【題目】設函數
有兩個零點
，
，且
.
（1）求
的求值范圍；
（2）求證：
.
【答案】(1)
;(2)見解析.
【解析】分析：（1）要保證函數
有兩個不同的零點
，
，可分析函數的單調性然后根據題意找出兩個不同兩點所對應的條件即可，對單調性的討論，注意a的影響；（2）由（1）可知，，是方程
（
）的兩個不等實根，也是方程
的兩個不等實根，也是函數
的兩個零點，且
，故再構造函數
，只需分析出
單調性即可得證.
（1）解法一：
.
①當
時，
，
在
上是增函數，不可能有兩個零點.
②當
時，由
，解得
，所以
若
，則
，所以在
上是減函數；若
，則，所以在
上是增函數.所以當時，取得極小值，也是它的最小值.
.
因為
，
，所以若使有兩個零點，只需
，解得
.
綜上，實數
的取值范圍是.
解法二：題意
方程有兩個不等實根，易知其中
，所以題意方程
有兩個不等實根函數
與
的圖象有兩個不同的公共點.
設
，則
，所以當
或
時，
，所以
在
和
上是減函數；當
，
，所以在
上是增函數，所以當
時，取得極小值
.
又因為
，
，
，
，在同一坐標系中分別畫出函數與的圖象，如圖所示，觀察圖形可知當時，二者有兩個不同的公共點.
所以實數的取值范圍是.
（2）證明：由（1）可知，，是方程（）的兩個不等實根，也是方程的兩個不等實根，也是函數的兩個零點，且.
因為
，所以當時，
，所以
在上是減函數；當時，
，所以在上是增函數.
設，則
，所以當時，
，所以在上是減函數，所以
，即
，即
，即
.
又因為
，所以
，所以
.
天天向上一本好卷系列答案
小學生10分鐘應用題系列答案科目：高中數學 來源： 題型：
【題目】已知橢圓
的右焦點為
，且點
在橢圓
上，
為坐標原點
（1）求橢圓的標準方程
（2）過橢圓
上異于其頂點的任一點
，作圓
的切線，切點分別為
（不在坐標軸上），若直線
的橫縱截距分別為
，求證：
為定值
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，橢圓
經過點
，且點
到橢圓的兩焦點的距離之和為
.
（l）求橢圓
的標準方程；
（2）若
是橢圓上的兩個點，線段
的中垂線
的斜率為
且直線與交于點
，
為坐標原點，求證：
三點共線．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知集合A={x||x﹣1|≤2，x∈Z}，B={x|y=log2（x+1），x∈R}，則A∩B=（ ）
A.{﹣1，0，1，2，3}
B.{0，1，2，3}
C.{1，2，3}
D.{﹣1，1，2，3}
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知直線l：x﹣y=1與圓Γ：x2+y2﹣2x+2y﹣1=0相交于A，C兩點，點B，D分別在圓Γ上運動，且位于直線l的兩側，則四邊形ABCD面積的最大值為（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知某算法的程序框圖如圖所示，若將輸出的(x，y)值依次記為(x1，y1)，(x2，y2)，…，(xn，yn)，….
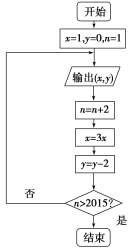
(1)若程序運行中輸出的一個數組是(9，t)，求t的值；
(2)程序結束時，共輸出(x，y)的組數為多少；
(3)寫出程序框圖的程序語句．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖所示，△ABC內接于圓O，D是 
的中點，∠BAC的平分線分別交BC和圓O于點E，F． （Ⅰ）求證：BF是△ABE外接圓的切線；
（Ⅱ）若AB=3，AC=2，求DB2﹣DA2的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】建造一間地面面積為12
的背面靠墻的豬圈, 底面為長方形的豬圈正面的造價為120元/, 側面的造價為80元/, 屋頂造價為1120元. 如果墻高3
, 且不計豬圈背面的費用, 問怎樣設計能使豬圈的總造價最低, 最低總造價是多少元?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
