
【題目】已知函數(shù)f(x)=|x﹣5|﹣|x﹣2|.
(1)若x∈R,使得f(x)≤m成立,求m的范圍;
(2)求不等式x2﹣8x+15+f(x)≤0的解集.
【答案】
(1)解: 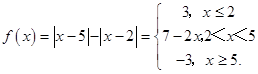 ,
,
當(dāng)2<x<5時,﹣3<7﹣2x<3,
所以﹣3≤f(x)≤3,
∴m≥﹣3
(2)解:不等式x2﹣8x+15+f(x)≤0,
即﹣f(x)≥x2﹣8x+15由(1)可知,
當(dāng)x≤2時,﹣f(x)≥x2﹣8x+15的解集為空集;
當(dāng)2<x<5時,﹣f(x)≥x2﹣8x+15,
即x2﹣10x+22≤0,∴ ![]() ;
;
當(dāng)x≥5時,﹣f(x)≥x2﹣8x+15,
即x2﹣8x+12≤0,∴5≤x≤6;
綜上,原不等式的解集為 ![]()
【解析】(1)通過討論x的范圍,求出f(x)的分段函數(shù)的形式,求出m的范圍即可;(2)通過討論x的范圍,求出不等式的解集即可.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】在直角坐標(biāo)系中,以原點為極點,x軸的正半軸為極軸建立坐標(biāo)系.已知曲線C:ρsin2θ=2acosθ(a>0),過點P(﹣2,﹣4)的直線l的參數(shù)方程為 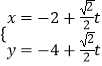 (t為參數(shù)),直線l與曲線C分別交于M、N兩點.
(t為參數(shù)),直線l與曲線C分別交于M、N兩點.
(1)寫出曲線C和直線l的普通方程;
(2)若|PM|,|MN|,|PN|成等比數(shù)列,求a的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】一箱方便面共有50袋,用隨機抽樣方法從中抽取了10袋,并稱其質(zhì)量(單位:g)結(jié)果為:60.5 61 60 60 61.5 59.5 59.5 58 60 60
(1)指出總體、個體、樣本、樣本容量;
(2)指出樣本數(shù)據(jù)的眾數(shù)、中位數(shù)、平均數(shù);
(3)求樣本數(shù)據(jù)的方差.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,某市準備在道路![]() 的一側(cè)修建一條運動比賽道,賽道的前一部分為曲線段
的一側(cè)修建一條運動比賽道,賽道的前一部分為曲線段![]() ,該曲線段是函數(shù)
,該曲線段是函數(shù)![]() ,
, ![]() 時的圖象,且圖象的最高點為
時的圖象,且圖象的最高點為![]() .賽道的中間部分為長
.賽道的中間部分為長![]() 千米的直線跑道
千米的直線跑道![]() ,且
,且![]() .賽道的后一部分是以
.賽道的后一部分是以![]() 為圓心的一段圓弧
為圓心的一段圓弧![]() .
.

(1)求![]() 的值和
的值和![]() 的大小;
的大小;
(2)若要在圓弧賽道所對應(yīng)的扇形![]() 區(qū)域內(nèi)建一個“矩形草坪”,矩形的一邊在道路
區(qū)域內(nèi)建一個“矩形草坪”,矩形的一邊在道路![]() 上,一個頂點在半徑
上,一個頂點在半徑![]() 上,另外一個頂點
上,另外一個頂點![]() 在圓弧
在圓弧![]() 上,且
上,且![]() ,求當(dāng)“矩形草坪”的面積取最大值時
,求當(dāng)“矩形草坪”的面積取最大值時![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
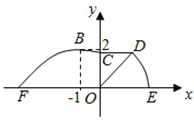
【題目】如圖,某市準備在道路![]() 的一側(cè)修建一條運動比賽道,賽道的前一部分為曲線段
的一側(cè)修建一條運動比賽道,賽道的前一部分為曲線段![]() ,該曲線段是函數(shù)
,該曲線段是函數(shù)![]() ,
, ![]() 時的圖象,且圖象的最高點為
時的圖象,且圖象的最高點為![]() .賽道的中間部分為長
.賽道的中間部分為長![]() 千米的直線跑道
千米的直線跑道![]() ,且
,且![]() .賽道的后一部分是以
.賽道的后一部分是以![]() 為圓心的一段圓弧
為圓心的一段圓弧![]() .
.
(1)求![]() 的值和
的值和![]() 的大小;
的大小;
(2)若要在圓弧賽道所對應(yīng)的扇形![]() 區(qū)域內(nèi)建一個“矩形草坪”,矩形的一邊在道路
區(qū)域內(nèi)建一個“矩形草坪”,矩形的一邊在道路![]() 上,一個頂點在半徑
上,一個頂點在半徑![]() 上,另外一個頂點
上,另外一個頂點![]() 在圓弧
在圓弧![]() 上,且
上,且![]() ,求當(dāng)“矩形草坪”的面積取最大值時
,求當(dāng)“矩形草坪”的面積取最大值時![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】下列說法正確的是( )
A.極坐標(biāo)系中方程ρ2﹣4ρcosθ=0和ρ﹣4cosθ=0表示的是同一曲線
B.![]()
C.不等式|a+b|≥|a|﹣|b|等號成立的條件為ab≤0
D.在極坐標(biāo)系中方程 ![]() 表示的圓和一條直線.
表示的圓和一條直線.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知實數(shù)x1 , x2 , x3 , x4 , x5滿足0<x1<x2<x3<x4<x5
(1)求證不等式x12+x22+x32+x42+x52>x1x2+x2x3+x3x4+x4x5+x5x1
(2)隨機變量X取值 ![]() 的概率均為
的概率均為 ![]() ,隨機變量Y取值
,隨機變量Y取值 ![]() 的概率也均為
的概率也均為 ![]() ,比較DX與DY大小關(guān)系.
,比較DX與DY大小關(guān)系.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知拋物線 ![]() ,焦點到準線的距離為4,過點
,焦點到準線的距離為4,過點 ![]() 的直線交拋物線于
的直線交拋物線于 ![]() 兩點.
兩點.
(Ⅰ)求拋物線的方程;
(Ⅱ)如果點 ![]() 恰是線段
恰是線段 ![]() 的中點,求直線
的中點,求直線 ![]() 的方程.
的方程.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com