
【題目】某市居民自來水收費標(biāo)準(zhǔn)如下:每戶每月用水不超過4噸時,每噸為![]() 元,當(dāng)用水超過4噸時,超過部分每噸為
元,當(dāng)用水超過4噸時,超過部分每噸為![]() 元,每月甲、乙兩戶共交水費
元,每月甲、乙兩戶共交水費![]() 元,已知甲、乙兩戶該月用水量分別為
元,已知甲、乙兩戶該月用水量分別為![]() .
.
(1)求![]() 關(guān)于
關(guān)于![]() 的函數(shù)關(guān)系式;
的函數(shù)關(guān)系式;
(2)若甲、乙兩戶該月共交水費![]() 元,分別求出甲、乙兩戶該月的用水量.
元,分別求出甲、乙兩戶該月的用水量.
【答案】(1)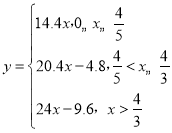 ;(2)甲戶用水量為7.5噸,乙戶用水量為4.5噸
;(2)甲戶用水量為7.5噸,乙戶用水量為4.5噸
【解析】
(1)由題意知:x≥0,令5x=4,得x=![]() ;令3x=4,得x=
;令3x=4,得x=![]() .將x取值范圍分三段,求對應(yīng)函數(shù)解析式可得答案.
.將x取值范圍分三段,求對應(yīng)函數(shù)解析式可得答案.
(2)在分段函數(shù)各定義域上討論函數(shù)值對應(yīng)的x的值.
(1)由題意知,x≥0,令5x=4,得x=![]() ;令3x=4,得x=
;令3x=4,得x=![]() .
.
則當(dāng)0≤x≤![]() 時,
時,
y=(5x+3x)×1.8=14.4x,
當(dāng)![]() <x≤
<x≤![]() 時,
時,
y=4×1.8+(x![]() )×5×3+3x1.8=20.4x4.8,
)×5×3+3x1.8=20.4x4.8,
當(dāng)x>![]() 時,y=(4+4)×1.8+(
時,y=(4+4)×1.8+(![]()
![]() )×5×3+3×5(x
)×5×3+3×5(x![]() )+3×3(x
)+3×3(x![]() )=24x9.6,
)=24x9.6,
即得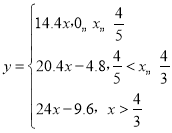 ;
;
(2)由于y=f(x)在各段區(qū)間上均單增,
當(dāng)0≤x≤![]() 時,y≤f(
時,y≤f(![]() )<26.4,
)<26.4,
當(dāng)![]() <x≤
<x≤![]() 時,y≤f(
時,y≤f(![]() )<26.4,
)<26.4,
當(dāng)x>![]() 時,令24x9.6=26.4,得x=1.5,
時,令24x9.6=26.4,得x=1.5,
所以甲戶用水量為5x=7.5噸,付費S1=4×1.8+3.5×3=17.70元
乙戶用水量為3x=4.5噸,付費S2=8.7元.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】中國有個名句“運籌帷幄之中,決勝千里之外”.其中的“籌”原意是指《孫 子算經(jīng)》中記載的算籌,古代是用算籌來進行計算,算籌是將幾寸長的小竹棍擺在平面上進行運算,算籌的擺放形式有縱橫兩種形式,如下表:
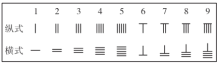
表示一個多位數(shù)時,像阿拉伯計數(shù)一樣,把各個數(shù)位的數(shù)碼從左到右排 列,但各位數(shù)碼的籌式需要縱橫相間,個位,百位,萬位用縱式表示,十位,千位,十萬位用橫式表示,以此類推,例如2268用算籌表示就是=||丄|||.執(zhí)行如圖所示程序框 圖,若輸人的x=1, y = 2,則輸出的S用算籌表示為![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,平面PAC⊥平面ABC,![]() 是以AC為斜邊的等腰直角三角形,E,F,O分別為PA,PB,AC的中點,
是以AC為斜邊的等腰直角三角形,E,F,O分別為PA,PB,AC的中點,![]() .
.

(1)設(shè)G是OC的中點,證明:![]() ∥平面
∥平面![]() ;
;
(2)證明:在![]() 內(nèi)存在一點M,使FM⊥平面BOE,求點M到OA,OB的距離.
內(nèi)存在一點M,使FM⊥平面BOE,求點M到OA,OB的距離.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知三棱錐![]() 底面的3個頂點
底面的3個頂點![]() 在球
在球![]() 的同一個大圓上,且
的同一個大圓上,且![]() 為正三角形,
為正三角形,![]() 為該球面上的點,若三棱錐
為該球面上的點,若三棱錐![]() 體積的最大值為
體積的最大值為![]() ,則球
,則球![]() 的表面積為( )
的表面積為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】每年10月中上旬是小麥的最佳種植時間,但小麥的發(fā)芽會受到土壤、氣候等多方面因素的影響.某科技小組為了解晝夜溫差的大小與小麥發(fā)芽的多少之間的關(guān)系,在不同的溫差下統(tǒng)計了100顆小麥種子的發(fā)芽數(shù),得到了如下數(shù)據(jù):
溫差 | 8 | 10 | 11 | 12 | 13 |
發(fā)芽數(shù) | 79 | 81 | 85 | 86 | 90 |
(1)請根據(jù)統(tǒng)計的最后三組數(shù)據(jù),求出![]() 關(guān)于
關(guān)于![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(2)若由(1)中的線性回歸方程得到的估計值與前兩組數(shù)據(jù)的實際值誤差均不超過兩顆,則認為線性回歸方程是可靠的,試判斷(1)中得到的線性回歸方程是否可靠;
(3)若100顆小麥種子的發(fā)芽率為![]() 顆,則記為
顆,則記為![]() 的發(fā)芽率,當(dāng)發(fā)芽率為
的發(fā)芽率,當(dāng)發(fā)芽率為![]() 時,平均每畝地的收益為
時,平均每畝地的收益為![]() 元,某農(nóng)場有土地10萬畝,小麥種植期間晝夜溫差大約為
元,某農(nóng)場有土地10萬畝,小麥種植期間晝夜溫差大約為![]() ,根據(jù)(1)中得到的線性回歸方程估計該農(nóng)場種植小麥所獲得的收益.
,根據(jù)(1)中得到的線性回歸方程估計該農(nóng)場種植小麥所獲得的收益.
附:在線性回歸方程![]() 中,
中,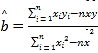 .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系![]() 中,直線
中,直線![]() 的參數(shù)方程為
的參數(shù)方程為![]() (
(![]() 為參數(shù),
為參數(shù),![]() ),曲線
),曲線![]() 的參數(shù)方程為
的參數(shù)方程為 (
(![]() 為參數(shù)),以坐標(biāo)原點為極點,
為參數(shù)),以坐標(biāo)原點為極點,![]() 軸的正半軸為極軸建立極坐標(biāo)系.
軸的正半軸為極軸建立極坐標(biāo)系.
(1)求曲線![]() 的極坐標(biāo)方程;
的極坐標(biāo)方程;
(2)設(shè)曲線![]() 與曲線
與曲線![]() 的交點分別為
的交點分別為![]() ,求
,求![]() 的最大值及此時直線
的最大值及此時直線![]() 的傾斜角.
的傾斜角.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,正三棱柱![]() 各條棱的長度均相等,
各條棱的長度均相等,![]() 為
為![]() 的中點,
的中點,![]() 分別是線段
分別是線段![]() 和線段
和線段![]() 的動點(含端點),且滿足
的動點(含端點),且滿足![]() ,當(dāng)
,當(dāng)![]() 運動時,下列結(jié)論中不正確的是
運動時,下列結(jié)論中不正確的是

A. 在![]() 內(nèi)總存在與平面
內(nèi)總存在與平面![]() 平行的線段
平行的線段
B. 平面![]() 平面
平面![]()
C. 三棱錐![]() 的體積為定值
的體積為定值
D. ![]() 可能為直角三角形
可能為直角三角形
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com