
【題目】已知![]() ,
,![]() .
.
⑴求![]() 的解析式;
的解析式;
⑵求![]() 時,
時,![]() 的值域;
的值域;
⑶設(shè)![]() ,若
,若![]() 對任意的
對任意的![]() ,總有
,總有![]() 恒成立,求實數(shù)
恒成立,求實數(shù)![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】
試題(1)由題已知![]() ,求
,求![]() ,可利用換元法,即:
,可利用換元法,即:![]() ,
,![]() ,將條件中的
,將條件中的![]() ,換為
,換為![]() 得:
得:![]() ,求出
,求出![]()
(2)由(1)得![]() ,可繼續(xù)換元,
,可繼續(xù)換元,![]()
得:![]() ,需對
,需對![]() 進行分類討論,而化為熟悉的二次函數(shù)的
進行分類討論,而化為熟悉的二次函數(shù)的
值域問題解決.
(3)由![]() 恒成立,可轉(zhuǎn)化為
恒成立,可轉(zhuǎn)化為![]() 在
在![]() 滿足
滿足![]() ,則需對
,則需對![]() 的單調(diào)性進行分析,由
的單調(diào)性進行分析,由![]() ,采用換元法
,采用換元法![]() ,得:
,得:
![]() ,由
,由![]() ,借助函數(shù)的單調(diào)性,對
,借助函數(shù)的單調(diào)性,對![]() 進行分類討論,分別得出
進行分類討論,分別得出![]() 的取值范圍,取各種情況的并集,得出結(jié)果.
的取值范圍,取各種情況的并集,得出結(jié)果.
試題解析:⑴設(shè)![]() ,則
,則![]() ,所以
,所以![]() ,
,
所以![]() ;
;
⑵設(shè)![]() ,則
,則![]()
當![]() 時,
時,![]() ,
,![]() 的值域為
的值域為![]()
當![]() 時,
時,![]()
若![]() ,
,![]() ,
,![]() 的值域為
的值域為![]()
若![]() ,
,![]() ,
,![]() 在
在![]() 上單調(diào)遞增,在
上單調(diào)遞增,在![]() 上單調(diào)遞減,
上單調(diào)遞減,
![]() 的值域為
的值域為![]()
綜上,當![]() 時
時![]() 的值域為
的值域為![]() ,當
,當![]() 時
時![]() 的值域為
的值域為![]() ;
;
⑶因為![]() 對任意
對任意![]() 總有
總有![]()
所以![]() 在
在![]() 滿足
滿足![]()
設(shè)![]() ,則
,則![]() ,
,![]()
當![]() 即
即![]() 時
時![]() 在區(qū)間
在區(qū)間![]() 單調(diào)遞增
單調(diào)遞增
所以![]() ,即
,即![]() ,所以
,所以![]() (舍)
(舍)
當![]() 時,
時,![]() ,不符合題意
,不符合題意
當![]() 時, 若
時, 若![]() 即
即![]() 時,
時,![]() 在區(qū)間
在區(qū)間![]() 單調(diào)遞增
單調(diào)遞增
所以![]() ,則
,則![]()
若![]() 即
即![]() 時
時![]() 在
在![]() 遞增,在
遞增,在![]() 遞減
遞減
所以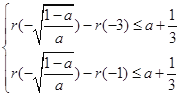 ,得
,得![]()
若![]() 即
即![]() 時
時![]() 在區(qū)間
在區(qū)間![]() 單調(diào)遞減
單調(diào)遞減
所以![]() ,即
,即![]() ,得
,得![]()
綜上所述:![]() .
.


 每日10分鐘口算心算速算天天練系列答案
每日10分鐘口算心算速算天天練系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)=x,g(x)=x-4,則下列結(jié)論正確的是( )
A.若h(x)=f(x)g(x),則函數(shù)h(x)的最小值為4
B.若h(x)=f(x)|g(x)|,則函數(shù)h(x)的值域為R
C.若h(x)=|f(x)|-|g(x)|,則函數(shù)h(x)有且僅有一個零點
D.若h(x)=|f(x)|-|g(x)|,則|h(x)|≤4恒成立
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某房產(chǎn)中介公司2017年9月1日正式開業(yè),現(xiàn)對其每個月的二手房成交量進行統(tǒng)計,![]() 表示開業(yè)第
表示開業(yè)第![]() 個月的二手房成交量,得到統(tǒng)計表格如下:
個月的二手房成交量,得到統(tǒng)計表格如下:

(1)統(tǒng)計中常用相關(guān)系數(shù)![]() 來衡量兩個變量之間線性關(guān)系的強弱.統(tǒng)計學(xué)認為,對于變量
來衡量兩個變量之間線性關(guān)系的強弱.統(tǒng)計學(xué)認為,對于變量![]() ,如果
,如果![]() ,那么相關(guān)性很強;如果
,那么相關(guān)性很強;如果![]() ,那么相關(guān)性一般;如果
,那么相關(guān)性一般;如果![]() ,那么相關(guān)性較弱.通過散點圖初步分析可用線性回歸模型擬合
,那么相關(guān)性較弱.通過散點圖初步分析可用線性回歸模型擬合![]() 與
與![]() 的關(guān)系.計算
的關(guān)系.計算![]() 的相關(guān)系數(shù)
的相關(guān)系數(shù)![]() ,并回答是否可以認為兩個變量具有很強的線性相關(guān)關(guān)系(計算結(jié)果精確到0.01)
,并回答是否可以認為兩個變量具有很強的線性相關(guān)關(guān)系(計算結(jié)果精確到0.01)
(2)請根據(jù)上表提供的數(shù)據(jù),用最小二乘法求出![]() 關(guān)于
關(guān)于![]() 的線性回歸方程
的線性回歸方程![]() (計算結(jié)果精確到0.01),并預(yù)測該房產(chǎn)中介公司2018年6月份的二手房成交量(計算結(jié)果四舍五入取整數(shù)).
(計算結(jié)果精確到0.01),并預(yù)測該房產(chǎn)中介公司2018年6月份的二手房成交量(計算結(jié)果四舍五入取整數(shù)).
(3)該房產(chǎn)中介為增加業(yè)績,決定針對二手房成交客戶開展抽獎活動.若抽中“一等獎”獲6千元獎金;抽中“二等獎”獲3千元獎金;抽中“祝您平安”,則沒有獎金.已知一次抽獎活動中獲得“一等獎”的概率為![]() ,獲得“二等獎”的概率為
,獲得“二等獎”的概率為![]() ,現(xiàn)有甲、乙兩個客戶參與抽獎活動,假設(shè)他們是否中獎相互獨立,求此二人所獲獎金總額
,現(xiàn)有甲、乙兩個客戶參與抽獎活動,假設(shè)他們是否中獎相互獨立,求此二人所獲獎金總額![]() (千元)的分布列及數(shù)學(xué)期望.
(千元)的分布列及數(shù)學(xué)期望.
參考數(shù)據(jù):![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
參考公式:
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】對于函數(shù)![]() ,若定義域內(nèi)存在實數(shù)
,若定義域內(nèi)存在實數(shù)![]() ,滿足
,滿足![]() ,則稱
,則稱![]() 為“局部奇函數(shù)”.
為“局部奇函數(shù)”.
(1)已知二次函數(shù)![]() ,試判斷
,試判斷![]() 是否為“局部奇函數(shù)”?并說明理由.
是否為“局部奇函數(shù)”?并說明理由.
(2)設(shè)![]() 是定義在
是定義在![]() 上的“局部奇函數(shù)”,求實數(shù)
上的“局部奇函數(shù)”,求實數(shù)![]() 的取值范圍;
的取值范圍;
(3)設(shè)![]() ,若
,若![]() 不是定義域R上的“局部奇函數(shù)”,求實數(shù)
不是定義域R上的“局部奇函數(shù)”,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】下列說法中錯誤的是__________(填序號)
①命題“![]() ,有
,有![]() ”的否定是“
”的否定是“![]() ”,有
”,有![]() ”;
”;
②已知![]() ,
, ![]() ,
, ![]() ,則
,則![]() 的最小值為
的最小值為![]() ;
;
③設(shè)![]() ,命題“若
,命題“若![]() ,則
,則![]() ”的否命題是真命題;
”的否命題是真命題;
④已知![]() ,
, ![]() ,若命題
,若命題![]() 為真命題,則
為真命題,則![]() 的取值范圍是
的取值范圍是![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】若函數(shù)![]() 的定義域為
的定義域為![]() ,滿足對任意
,滿足對任意![]() ,有
,有![]() .則稱
.則稱![]() 為“
為“![]() 形函數(shù)”;若函數(shù)
形函數(shù)”;若函數(shù)![]() 定義域為
定義域為![]() ,
,![]() 恒大于0,且對任意
恒大于0,且對任意![]() ,恒有
,恒有![]() ,則稱
,則稱![]() 為“對數(shù)
為“對數(shù)![]() 形函數(shù)”.
形函數(shù)”.
(1)當![]() 時,判斷
時,判斷![]() 是否是“
是否是“![]() 形函數(shù)”,并說明理由;
形函數(shù)”,并說明理由;
(2)當![]() 時,判斷
時,判斷![]() 是否是“對數(shù)
是否是“對數(shù)![]() 形函數(shù)”,并說明理由;
形函數(shù)”,并說明理由;
(3)若函數(shù)![]() 是
是![]() 形函數(shù),且滿足對任意
形函數(shù),且滿足對任意![]() 都有
都有![]() ,問
,問![]() 是否是“對數(shù)
是否是“對數(shù)![]() 形函數(shù)”?請加以證明,如果不是,請說明理由.
形函數(shù)”?請加以證明,如果不是,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】若![]() 的展開式中,第二、三、四項的二項式系數(shù)成等差數(shù)列.
的展開式中,第二、三、四項的二項式系數(shù)成等差數(shù)列.
(1)求![]() 的值;
的值;
(2)此展開式中是否有常數(shù)項,為什么?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)拋物線![]() 的焦點為
的焦點為![]() ,過點
,過點![]() 作垂直于
作垂直于![]() 軸的直線與拋物線交于
軸的直線與拋物線交于![]() ,
,![]() 兩點,且以線段
兩點,且以線段![]() 為直徑的圓過點
為直徑的圓過點![]() .
.
(1)求拋物線![]() 的方程;
的方程;
(2)若直線![]() 與拋物線
與拋物線![]() 交于
交于![]() ,
,![]() 兩點,點
兩點,點![]() 為曲線
為曲線![]() :
:![]() 上的動點,求
上的動點,求![]() 面積的最小值.
面積的最小值.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com