
【題目】設數列![]() (
(![]() )的各項均為正整數,且
)的各項均為正整數,且![]() .若對任意
.若對任意![]() ,存在正整數
,存在正整數![]() 使得
使得![]() ,則稱數列
,則稱數列![]() 具有性質
具有性質![]() .
.
(1)判斷數列![]() 與數列
與數列![]() 是否具有性質
是否具有性質![]() ;(只需寫出結論)
;(只需寫出結論)
(2)若數列![]() 具有性質
具有性質![]() ,且
,且![]() ,
,![]() ,
,![]() ,求
,求![]() 的最小值;
的最小值;
(3)若集合![]() ,且
,且![]() (任意
(任意![]() ,
,![]() ).求證:存在
).求證:存在![]() ,使得從
,使得從![]() 中可以選取若干元素(可重復選取)組成一個具有性質
中可以選取若干元素(可重復選取)組成一個具有性質![]() 的數列.
的數列.
【答案】(1)數列![]() 不具有性質
不具有性質![]() ;數列
;數列![]() 具有性質
具有性質![]() (2)
(2)![]() 的最小值為
的最小值為![]() (3)證明見解析
(3)證明見解析
【解析】
(1)![]() 不滿足存在正整數
不滿足存在正整數![]() 使得
使得![]() ,故數列
,故數列![]() 不具有性質
不具有性質![]() ;根據定義可知數列
;根據定義可知數列![]() 具有性質
具有性質![]() ;
;
(2)由題可知![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,所以
,所以![]() ,再驗證可知
,再驗證可知![]() 時,數列
時,數列![]() 不具有性質
不具有性質![]() ,
,![]() 時,數列
時,數列![]() 具有性質
具有性質![]() ,從而可知
,從而可知![]() 的最小值為
的最小值為![]() ;
;
(3)反證法:假設結論不成立,即對任意![]() 都有:若正整數
都有:若正整數![]() ,則
,則![]() ,再根據定義推出矛盾,從而可證結論正確.
,再根據定義推出矛盾,從而可證結論正確.
(1)數列![]() 不具有性質
不具有性質![]() ;數列
;數列![]() 具有性質
具有性質![]() .
.
(2)由題可知![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]() .
.
若![]() ,因為
,因為![]() 且
且![]() ,所以
,所以![]() .
.
同理,![]()
因為數列各項均為正整數,所以![]() .所以數列前三項為
.所以數列前三項為![]() .
.
因為數列![]() 具有性質
具有性質![]() ,
,![]() 只可能為
只可能為![]() 之一,而又因為
之一,而又因為![]() ,
,
所以![]() .
.
同理,有![]() .
.
此時數列為![]() .
.
但數列中不存在![]() 使得
使得![]() ,所以該數列不具有性質
,所以該數列不具有性質![]() .
.
所以![]() .
.
當![]() 時,取
時,取![]() .(構造數列不唯一)
.(構造數列不唯一)
經驗證,此數列具有性質![]() .
.
所以,![]() 的最小值為
的最小值為![]() .
.
(3)反證法:假設結論不成立,即對任意![]() 都有:若正整數
都有:若正整數![]() ,則
,則![]() .
.
否則,存在![]() 滿足:存在
滿足:存在![]() ,
,![]() 使得
使得![]() ,此時,從
,此時,從![]() 中取出
中取出![]() :
:
當![]() 時,
時,![]() 是一個具有性質
是一個具有性質![]() 的數列;
的數列;
當![]() 時,
時,![]() 是一個具有性質
是一個具有性質![]() 的數列;
的數列;
當![]() 時,
時,![]() 是一個具有性質
是一個具有性質![]() 的數列.
的數列.
(i)由題意可知,這![]() 個集合中至少有一個集合的元素個數不少于
個集合中至少有一個集合的元素個數不少于![]() 個,
個,
不妨設此集合為![]() ,從
,從![]() 中取出
中取出![]() 個數,記為
個數,記為![]() ,且
,且![]() .
.
令集合![]() .
.
由假設,對任意![]() ,
,![]() ,所以
,所以![]() .
.
(ii)在![]() 中至少有一個集合包含
中至少有一個集合包含![]() 中的至少
中的至少![]() 個元素,不妨設這個集合為
個元素,不妨設這個集合為![]() ,
,
從![]() 中取出
中取出![]() 個數,記為
個數,記為![]() ,且
,且![]() .
.
令集合![]() .
.
由假設![]() .對任意
.對任意![]() ,存在
,存在![]() 使得
使得![]() .
.
所以對任意![]() ,
,![]() ,
,
由假設![]() ,所以
,所以![]() ,所以
,所以![]() ,所以
,所以![]() .
.
(iii)在![]() 中至少有一個集合包含
中至少有一個集合包含![]() 中的至少
中的至少![]() 個元素,不妨設這個集合為
個元素,不妨設這個集合為![]() ,
,
從![]() 中取出
中取出![]() 個數,記為
個數,記為![]() ,且
,且![]() .
.
令集合![]() .
.
由假設![]() .對任意
.對任意![]() ,存在
,存在![]() 使得
使得![]() .
.
所以對任意![]() ,
,![]() ,
,
同樣,由假設可得![]() ,所以
,所以![]() ,所以
,所以![]() .
.
(iv)類似地,在![]() 中至少有一個集合包含
中至少有一個集合包含![]() 中的至少
中的至少![]() 個元素,不妨設這個集合為
個元素,不妨設這個集合為![]() ,
,
從![]() 中取出
中取出![]() 個數,記為
個數,記為![]() ,且
,且![]() ,
,
則![]() .
.
(v)同樣,在![]() 中至少有一個集合包含
中至少有一個集合包含![]() 中的至少
中的至少![]() 個元素,不妨設這個集合為
個元素,不妨設這個集合為![]() ,
,
從![]() 中取出
中取出![]() 個數,記為
個數,記為![]() ,且
,且![]() ,同理可得
,同理可得![]() .
.
(vi)由假設可得![]() .
.
同上可知,![]() ,
,
而又因為![]() ,所以
,所以![]() ,矛盾.所以假設不成立.
,矛盾.所以假設不成立.
所以原命題得證.


 新課標快樂提優暑假作業陜西旅游出版社系列答案
新課標快樂提優暑假作業陜西旅游出版社系列答案科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,直線l的參數方程為![]() (t為參數),若以O為極點,x軸的正半軸為極軸且取相同的單位長度建立極坐標系,曲線C的極坐標方程為
(t為參數),若以O為極點,x軸的正半軸為極軸且取相同的單位長度建立極坐標系,曲線C的極坐標方程為![]() .
.
(1)求曲線C的直角坐標方程及直線l的普通方程;
(2)將所得曲線C向右平移1個單位長度,再將曲線C上的所有點的橫坐標變為原來的2倍,得到曲線![]() ,求曲線
,求曲線![]() 上的點到直線l的距離的最大值.
上的點到直線l的距離的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的普通方程為:
的普通方程為:![]() ,以坐標原點為極點,
,以坐標原點為極點,![]() 軸的正半軸為極軸建立極坐標系,曲線
軸的正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() ,正方形
,正方形![]() 的頂點都在
的頂點都在![]() 上,且
上,且![]() 逆時針依次排列,點
逆時針依次排列,點![]() 的極坐標為
的極坐標為![]()
(1)寫出曲線![]() 的參數方程,及點
的參數方程,及點![]() 的直角坐標;
的直角坐標;
(2)設![]() 為橢圓
為橢圓![]() 上的任意一點,求:
上的任意一點,求:![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,設點![]() 是拋物線
是拋物線![]() 的焦點,直線
的焦點,直線![]() 與拋物線
與拋物線![]() 相切于點
相切于點![]() (點
(點![]() 位于第一象限),并與拋物線
位于第一象限),并與拋物線![]() 的準線相交于點
的準線相交于點![]() .過點
.過點![]() 且與直線
且與直線![]() 垂直的直線
垂直的直線![]() 交拋物線
交拋物線![]() 于另一點
于另一點![]() ,交
,交![]() 軸于點
軸于點![]() ,連結
,連結![]() .
.
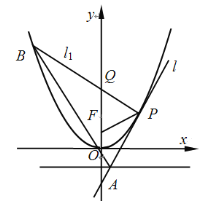
(1)證明:![]() 為等腰三角形;
為等腰三角形;
(2)求![]() 面積的最小值.
面積的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】數學中有許多寓意美好的曲線,曲線![]() 被稱為“四葉玫瑰線”(如圖所示).
被稱為“四葉玫瑰線”(如圖所示).

給出下列三個結論:
①曲線![]() 關于直線
關于直線![]() 對稱;
對稱;
②曲線![]() 上任意一點到原點的距離都不超過
上任意一點到原點的距離都不超過![]() ;
;
③存在一個以原點為中心、邊長為![]() 的正方形,使得曲線
的正方形,使得曲線![]() 在此正方形區域內(含邊界).
在此正方形區域內(含邊界).
其中,正確結論的序號是________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列結論中正確的個數是( )
①在![]() 中,“
中,“![]() ”是“
”是“![]() ”的必要不充分條件;
”的必要不充分條件;
②若![]() ,
,![]() 的最小值為2;
的最小值為2;
③夾在圓柱的兩個平行截面間的幾何體是圓柱;
④數列![]() 的通項公式為
的通項公式為![]() ,則數列的前
,則數列的前![]() 項和
項和![]() .( )
.( )
A.0B.1C.2D.3
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了實施“科技下鄉,精準脫貧”戰略,某縣科技特派員帶著![]() 三個農業扶貧項目進駐某村,對僅有的四個貧困戶進行產業幫扶.經過前期走訪得知,這四個貧困戶甲、乙、丙、丁選擇
三個農業扶貧項目進駐某村,對僅有的四個貧困戶進行產業幫扶.經過前期走訪得知,這四個貧困戶甲、乙、丙、丁選擇![]() 三個項目的意向如下:
三個項目的意向如下:
扶貧項目 |
|
|
|
貧困戶 | 甲、乙、丙、丁 | 甲、乙、丙 | 丙、丁 |
若每個貧困戶只能從自己已登記的選擇意向中隨機選取一項,且每個項目至多有兩個貧困戶選擇,則甲乙兩戶選擇同一個扶貧項目的概率為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】近期,西安公交公司分別推出支付寶和微信掃碼支付乘車活動,活動設置了一段時間的推廣期,由于推廣期內優惠力度較大,吸引越來越多的人開始使用掃碼支付.某線路公交車隊統計了活動剛推出一周內每一天使用掃碼支付的人次,![]() 表示活動推出的天數,
表示活動推出的天數,![]() 表示每天使用掃碼支付的人次(單位:十人次),統計數據如表下所示:
表示每天使用掃碼支付的人次(單位:十人次),統計數據如表下所示:
![]()
根據以上數據,繪制了散點圖.
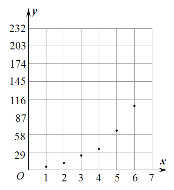
(1)根據散點圖判斷,在推廣期內,![]() 與
與![]() (
(![]() 均為大于零的常數),哪一個適宜作為掃碼支付的人次
均為大于零的常數),哪一個適宜作為掃碼支付的人次![]() 關于活動推出天數
關于活動推出天數![]() 的回歸方程類型?(給出判斷即可,不必說明理由);
的回歸方程類型?(給出判斷即可,不必說明理由);
(2)根據(1)的判斷結果及表1中的數據,建立![]() 與
與![]() 的回歸方程,并預測活動推出第8天使用掃碼支付的人次;
的回歸方程,并預測活動推出第8天使用掃碼支付的人次;
(3)推廣期結束后,車隊對乘客的支付方式進行統計,結果如下表:
![]()
西安公交六公司車隊為緩解周邊居民出行壓力,以![]() 萬元的單價購進了一批新車,根據以往的經驗可知,每輛車每個月的運營成本約為
萬元的單價購進了一批新車,根據以往的經驗可知,每輛車每個月的運營成本約為![]() 萬元.已知該線路公交車票價為
萬元.已知該線路公交車票價為![]() 元,使用現金支付的乘客無優惠,使用乘車卡支付的乘客享受
元,使用現金支付的乘客無優惠,使用乘車卡支付的乘客享受![]() 折優惠,掃碼支付的乘客隨機優惠,根據統計結果得知,使用掃碼支付的乘客中有
折優惠,掃碼支付的乘客隨機優惠,根據統計結果得知,使用掃碼支付的乘客中有![]() 的概率享受
的概率享受![]() 折優惠,有
折優惠,有![]() 的概率享受
的概率享受![]() 折優惠,有
折優惠,有![]() 的概率享受
的概率享受![]() 折優惠.預計該車隊每輛車每個月有
折優惠.預計該車隊每輛車每個月有![]() 萬人次乘車,根據所給數據以事件發生的頻率作為相應事件發生的概率,在不考慮其它因素的條件下,按照上述收費標準,假設這批車需要
萬人次乘車,根據所給數據以事件發生的頻率作為相應事件發生的概率,在不考慮其它因素的條件下,按照上述收費標準,假設這批車需要![]() (
(![]() )年才能開始盈利,求
)年才能開始盈利,求![]() 的值.
的值.
參考數據:
|
|
|
|
|
|
|
|
|
|
其中其中![]() ,
,![]() ,
,
參考公式:對于一組數據![]() ,
,![]() ,
,![]() ,
,![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計公式分別為:
的斜率和截距的最小二乘估計公式分別為: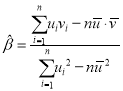 ,
,![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com