
|
(1)證明:![]() 平面
平面![]()

![]()

|
|
|
|
|
|
|
|
(1)證明:連結AD1交A1D于O,連結EO,則O為AD1的中點,又因為E是AB的中點,
所以OE∥BD1.
又∵![]() 平面A1DE BD1
平面A1DE BD1![]() 平面A1DE ∴BD1∥平面A1DE ……………………4分
平面A1DE ∴BD1∥平面A1DE ……………………4分
(2)證明:由題可知:四邊形ADD1A1是正方形
∴A1D⊥AD1 又∵AB⊥平面ADD1A1,A1D![]() 平面ADD1A1
平面ADD1A1
∴AB⊥AD1 又∵AB![]() 平面AD1E,AD1
平面AD1E,AD1![]() 平面A D1E AB
平面A D1E AB![]() AD1=A
AD1=A
∴A1D⊥平面AD1E 又∵D1E![]() 平面AD1E ∴A1D⊥D1E ………………………8分
平面AD1E ∴A1D⊥D1E ………………………8分
(3)解:在△CED中,CD=2,![]() ,
,![]()
CD2=CE2+DE2 ∴CE⊥DE。
又∵D1D⊥平面ABCD CE![]() 平面ABCD ∴CE⊥D1D
平面ABCD ∴CE⊥D1D
又∵![]() 平面D1DE DE
平面D1DE DE![]() 平面D1DE D1D
平面D1DE D1D![]() DE=D
DE=D
∴CE⊥平面D1DE 又∵D1E⊥平面D1DE,∴CE⊥D1E.
∴∠D1ED是二面角D1—ED—D的一個平面角.
在△D1ED中,∠D1DE=90°,D1D=1, DE=![]()
∴![]() ∴二面角D1—ED—D的正切值是
∴二面角D1—ED—D的正切值是![]() …………12分
…………12分


 手拉手全優練考卷系列答案
手拉手全優練考卷系列答案科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
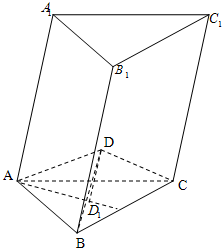 已知三棱錐D-ABC,D1為底面△ABC的重心,過A、B、C分別作DD1的平行線分別交對面所在的平面于A1,B1,C1點.(如,過A點作DD1的平行線交BCD所在的平面于A1點)
已知三棱錐D-ABC,D1為底面△ABC的重心,過A、B、C分別作DD1的平行線分別交對面所在的平面于A1,B1,C1點.(如,過A點作DD1的平行線交BCD所在的平面于A1點)查看答案和解析>>
科目:高中數學 來源: 題型:
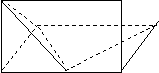
 (2013•湖北)如圖,某地質隊自水平地面A,B,C三處垂直向地下鉆探,自A點向下鉆到A1處發現礦藏,再繼續下鉆到A2處后下面已無礦,從而得到在A處正下方的礦層厚度為A1A2=d1.同樣可得在B,C處正下方的礦層厚度分別為B1B2=d2,C1C2=d3,且d1<d2<d3.過AB,AC的中點M,N且與直線AA2平行的平面截多面體A1B1C1-A2B2C2所得的截面DEFG為該多面體的一個中截面,其面積記為S中.
(2013•湖北)如圖,某地質隊自水平地面A,B,C三處垂直向地下鉆探,自A點向下鉆到A1處發現礦藏,再繼續下鉆到A2處后下面已無礦,從而得到在A處正下方的礦層厚度為A1A2=d1.同樣可得在B,C處正下方的礦層厚度分別為B1B2=d2,C1C2=d3,且d1<d2<d3.過AB,AC的中點M,N且與直線AA2平行的平面截多面體A1B1C1-A2B2C2所得的截面DEFG為該多面體的一個中截面,其面積記為S中.| 1 | 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:
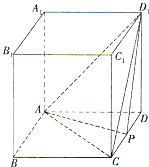 如圖,正方體ABCD-A1B1C1D1的棱長為2,P為棱CD上的一點,且三棱錐A-CP D1的體積為
如圖,正方體ABCD-A1B1C1D1的棱長為2,P為棱CD上的一點,且三棱錐A-CP D1的體積為| 2 | 3 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com