
【題目】如圖,在直角梯形![]() 中,
中,![]() ,且
,且![]() 分別為線段
分別為線段![]() 的中點,沿
的中點,沿![]() 把
把![]() 折起,使
折起,使![]() ,得到如下的立體圖形.
,得到如下的立體圖形.
(1)證明:平面![]() 平面
平面![]() ;
;
(2)若![]() ,求點
,求點![]() 到平面
到平面![]() 的距離.
的距離.

 名校課堂系列答案
名校課堂系列答案科目:高中數(shù)學(xué) 來源: 題型:
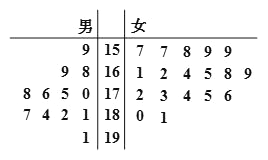
【題目】某學(xué)校在學(xué)校內(nèi)招募了![]() 名男志愿者和
名男志愿者和![]() 名女志愿者.將這
名女志愿者.將這![]() 名志愿者的身高編成如右莖葉圖(單位:
名志愿者的身高編成如右莖葉圖(單位: ![]() ),若身高在
),若身高在![]() 以上(包括
以上(包括![]() )定義為“高個子”,身高在
)定義為“高個子”,身高在![]() 以下(不包括
以下(不包括![]() )定義為“非高個子”,且只有“女高個子”才能擔(dān)任“禮儀小姐”.
)定義為“非高個子”,且只有“女高個子”才能擔(dān)任“禮儀小姐”.
(Ⅰ)如果用分層抽樣的方法從“高個子”和“非高個子”中抽取![]() 人,再從這
人,再從這![]() 人中選
人中選![]() 人,那么至少有一人是“高個子”的概率是多少?
人,那么至少有一人是“高個子”的概率是多少?
(Ⅱ)若從所有“高個子”中選![]() 名志愿者,用
名志愿者,用![]() 表示所選志愿者中能擔(dān)任“禮儀小姐”的人數(shù),試寫出
表示所選志愿者中能擔(dān)任“禮儀小姐”的人數(shù),試寫出![]() 的分布列,并求
的分布列,并求![]() 的數(shù)學(xué)期望.
的數(shù)學(xué)期望.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
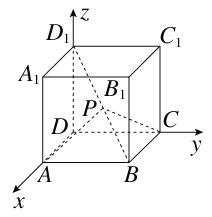
【題目】設(shè)動點P在棱長為1的正方體ABCD-A1B1C1D1的對角線BD1上,記![]() =λ.當(dāng)∠APC為鈍角時,λ的取值范圍是________.
=λ.當(dāng)∠APC為鈍角時,λ的取值范圍是________.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)數(shù)列![]() 的前n項和為
的前n項和為![]() ,對任意的正整數(shù)n,都有
,對任意的正整數(shù)n,都有![]() 成立,記
成立,記![]() (
(![]() ),
),
(1)求數(shù)列![]() 的通項公式;
的通項公式;
(2)記![]() (
(![]() ),設(shè)數(shù)列
),設(shè)數(shù)列![]() 的前n和為
的前n和為![]() ,求證:對任意正整數(shù)n,都有
,求證:對任意正整數(shù)n,都有![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知數(shù)列![]() 的前
的前![]() 項和為
項和為![]() ,滿足
,滿足![]() (
(![]() ),數(shù)列
),數(shù)列![]() 滿足
滿足![]() (
(![]() ),且
),且![]()
(1)證明數(shù)列![]() 為等差數(shù)列,并求數(shù)列
為等差數(shù)列,并求數(shù)列![]() 和
和![]() 的通項公式;
的通項公式;
(2)若![]() ,求數(shù)列
,求數(shù)列![]() 的前
的前![]() 項和
項和![]() ;
;
(3)若![]() ,數(shù)列
,數(shù)列![]() 的前
的前![]() 項和為
項和為![]() ,對任意的
,對任意的![]() ,都有
,都有![]() ,求實數(shù)
,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,且
,且![]() 過點
過點![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)若直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 兩點(點
兩點(點![]() 均在第一象限),且直線
均在第一象限),且直線![]() 的斜率成等比數(shù)列,證明:直線
的斜率成等比數(shù)列,證明:直線![]() 的斜率為定值.
的斜率為定值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】四棱錐![]() 的底面ABCD是邊長為2的菱形,側(cè)面PAD是正三角形,
的底面ABCD是邊長為2的菱形,側(cè)面PAD是正三角形,![]() ,E為AD的中點,二面角
,E為AD的中點,二面角![]() 為
為![]() .
.

![]() 證明:
證明:![]() 平面PBE;
平面PBE;
![]() 求點P到平面ABCD的距離;
求點P到平面ABCD的距離;
![]() 求直線BC與平面PAB所成角的正弦值.
求直線BC與平面PAB所成角的正弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知直線![]() :
:![]() ,若存在實數(shù)
,若存在實數(shù)![]() 使得一條曲線與直線
使得一條曲線與直線![]() 有兩個不同的交點,且以這兩個交點為端點的線段長度恰好等于
有兩個不同的交點,且以這兩個交點為端點的線段長度恰好等于![]() ,則稱此曲線為直線
,則稱此曲線為直線![]() 的“絕對曲線”.下面給出的四條曲線方程:
的“絕對曲線”.下面給出的四條曲線方程:
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .
.
其中直線![]() 的“絕對曲線”的條數(shù)為( )
的“絕對曲線”的條數(shù)為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系![]() 中,O為坐標(biāo)原點,以O為圓心的圓與直線
中,O為坐標(biāo)原點,以O為圓心的圓與直線![]() 相切.
相切.
(1)求圓O的方程.
(2)直線![]() 與圓O交于A,B兩點,在圓O上是否存在一點M,使得四邊形
與圓O交于A,B兩點,在圓O上是否存在一點M,使得四邊形![]() 為菱形?若存在,求出此時直線l的斜率;若不存在,說明理由.
為菱形?若存在,求出此時直線l的斜率;若不存在,說明理由.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com