
【題目】設函數f(x)=lg(﹣x2+5x﹣6)的定義域為A,函數g(x)![]() ,x∈(0,m)的值域為B.
,x∈(0,m)的值域為B.
(1)當m=2時,求A∩B;
(2)若“x∈A”是“x∈B”的必要不充分條件,求實數m的取值范圍.
【答案】(1)A∩B=(2,![]() )(2)(0,
)(2)(0,![]() ]
]
【解析】
(1)解一元二次不等式求得集合![]() ,當
,當![]() 時,利用
時,利用![]() 的單調性求得
的單調性求得![]() 的值域,也即求得集合
的值域,也即求得集合![]() ,由此求得兩個集合的交集.
,由此求得兩個集合的交集.
(2)根據![]() 的單調性求得
的單調性求得![]() 的值域,根據必要不充分條件的知識,判斷出
的值域,根據必要不充分條件的知識,判斷出![]() 是
是![]() 的真子集,由此列不等式組,解不等式組求得
的真子集,由此列不等式組,解不等式組求得![]() 的取值范圍.
的取值范圍.
(1)由﹣x2+5x﹣6>0,即x2﹣5x+6<0,解得2<x<3,即A=(2,3),
當m=2時,g(x)![]() ,x∈(0,2)上為減函數,
,x∈(0,2)上為減函數,
∴![]() g(x)
g(x)![]() ,即B=(
,即B=(![]() ,
,![]() ),
),
則A∩B=(2,![]() );
);
(2)∵g(x)![]() ,x∈(0,m)上為減函數,
,x∈(0,m)上為減函數,
∴![]() g(x)
g(x)![]() ,即B=(
,即B=(![]() ,
,![]() )
)
若“x∈A”是“x∈B”的必要不充分條件,
則![]() 是
是![]() 的真子集,
的真子集,
即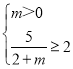 ,則
,則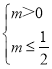 ,
,
即0<m![]() ,
,
故實數m的取值范圍是(0,![]() ].
].


 習題精選系列答案
習題精選系列答案科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
,![]() .
.
(![]() )設曲線
)設曲線![]() 在
在![]() 處的切線為
處的切線為![]() ,到點
,到點![]() 的距離為
的距離為![]() ,求
,求![]() 的值.
的值.
(![]() )若對于任意實數
)若對于任意實數![]() ,
,![]() 恒成立,試確定
恒成立,試確定![]() 的取值范圍.
的取值范圍.
(![]() )當
)當![]() 時,是否存在實數
時,是否存在實數![]() ,使曲線
,使曲線![]() 在點
在點![]() 處的切線與
處的切線與![]() 軸垂直?若存在,求出
軸垂直?若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C:![]() 的離心率
的離心率![]() ,連接橢圓的四個頂點得到的菱形的面積為
,連接橢圓的四個頂點得到的菱形的面積為![]() .
.

![]() 求橢圓C的方程;
求橢圓C的方程;
![]() 如圖所示,該橢圓C的左、右焦點
如圖所示,該橢圓C的左、右焦點![]() ,
,![]() 作兩條平行的直線分別交橢圓于A,B,C,D四個點,試求平行四邊形ABCD面積的最大值.
作兩條平行的直線分別交橢圓于A,B,C,D四個點,試求平行四邊形ABCD面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某蔬果經銷商銷售某種蔬果,售價為每公斤25元,成本為每公斤15元.銷售宗旨是當天進貨當天銷售.如果當天賣不出去,未售出的全部降價以每公斤10元處理完.根據以往的銷售情況,得到如圖所示的頻率分布直方圖:

(1)根據頻率分布直方圖計算該種蔬果日需求量的平均數![]() (同一組中的數據用該組區間中點值代表);
(同一組中的數據用該組區間中點值代表);
(2)該經銷商某天購進了250公斤這種蔬果,假設當天的需求量為![]() 公斤
公斤![]() ,利潤為
,利潤為![]() 元.求
元.求![]() 關于
關于![]() 的函數關系式,并結合頻率分布直方圖估計利潤
的函數關系式,并結合頻率分布直方圖估計利潤![]() 不小于1750元的概率.
不小于1750元的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】天壇公園是明、清兩代皇帝“祭天”“祈谷”的場所.天壇公園中的圜丘臺共有三層(如圖1所示),上層壇的中心是一塊呈圓形的大理石板,從中心向外圍以扇面形石(如圖2所示).上層壇從第一環至第九環共有九環,中層壇從第十環至第十八環共有九環,下層壇從第十九環至第二十七環共有九環;第一環的扇面形石有9塊,從第二環起,每環的扇面形石塊數比前一環多9塊,則第二十七環的扇面形石塊數是______;上、中、下三層壇所有的扇面形石塊數是_______.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,直三棱柱ABC﹣A1B1C1中,AC=BC=AA1=3,AC⊥BC,點M在線段AB上.
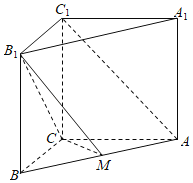
(1)若M是AB中點,證明AC1∥平面B1CM;
(2)當BM![]() 時,求直線C1A1與平面B1MC所成角的正弦值.
時,求直線C1A1與平面B1MC所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱錐![]() 中,已知
中,已知![]() 是正三角形,平面
是正三角形,平面![]() 平面
平面![]() ,
,![]() ,
,![]() 為
為![]() 的中點,
的中點,![]() 在棱
在棱![]() 上,且
上,且![]() .
.
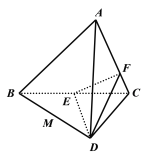
(1)求證:![]() 平面
平面![]() ;
;
(2)若![]() 為
為![]() 的中點,問
的中點,問![]() 上是否存在一點
上是否存在一點![]() ,使
,使![]() 平面
平面![]() ?若存在,說明點
?若存在,說明點![]() 的位置;若不存在,試說明理由.
的位置;若不存在,試說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com