【題目】已知圓 
的圓心為原點 ，且與直線 
相切。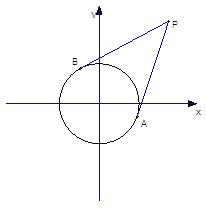 
（1）求圓 的方程；
（2）過點 
(8,6)引圓O的兩條切線 
，切點為 
，求直線 
的方程.
【答案】
（1）依題意得：圓 的半徑 
，
所以圓 的方程為 。
（2） 是圓 的兩條切線， 。 在以 為直徑的圓上。點 的坐標為 ，則線段 的中點坐標為 。
以 為直徑的圓方程為
化簡得： , 為兩圓的公共弦，
直線 的方程為 即 
。
【解析】分析：本題主要考查了圓的切線方程、直線與圓的位置關(guān)系、相交弦所在直線的方程，解決問題的關(guān)鍵是(1)根據(jù)弦心距關(guān)系求得半徑即可解決問題；(2)根據(jù) 
是圓 
的兩條切線，得到 
，所以 
在以 
為直徑的圓上，根據(jù)所給條件可得一 為直徑的圓方程為 
,聯(lián)立兩圓方程可得公共弦所在直線方程，
口算心算速算應(yīng)用題系列答案
同步拓展閱讀系列答案科目：高中數(shù)學(xué) 來源： 題型：
【題目】若二次函數(shù)f（x）=ax2+bx+c（a，b，c∈R）滿足f（x+1）﹣f（x）=4x+1，且f（0）=3．
（1）求f（x）的解析式；
（2）若在區(qū)間[﹣1，1]上，不等式f（x）＞6x+m恒成立，求實數(shù)m的取值范圍．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知命題P：4x﹣a2x+1≥0對x∈[﹣1，1]恒成立，命題Q：f（x）=log2（ax2﹣2x+ 
）的值域是R，若滿足P且Q為假，P或Q為真，求實數(shù)a的取值范圍．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知圓心在 
軸上的圓 
過點 
和 
，圓 
的方程為 
．
（1）求圓 的方程；
（2）由圓 上的動點 
向圓 作兩條切線分別交 
軸于 
， 
兩點，求 
的取值范圍．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)f（x）=|x|，g（x）=﹣|x﹣4|+m．
（1）解關(guān)于x的不等式g[f（x）]+3﹣m＞0；
（2）若函數(shù)f（x）的圖象恒在函數(shù)g（2x）圖象的上方，求實數(shù)m的取值范圍．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)f（x）+2= 
，當x∈（0，1]時，f（x）=x2 ， 若在區(qū)間（﹣1，1]內(nèi)，g（x）=f（x）﹣t（x+2）有兩個不同的零點，則實數(shù)t的取值范圍是（ ）
A.（0， 
]
B.（0， 
]
C.[﹣ ， ]
D.[﹣ ， ]
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】如圖，直線AB經(jīng)過⊙O上的點C，并且OA=OB，CA=CB，⊙O交直線OB于E、D，連接EC、CD．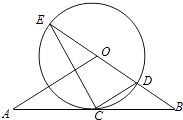 
（1）求證：直線AB是⊙O的切線；
（2）若tan∠CED= 
，⊙O的半徑為3，求OA的長．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】選修4-4：坐標系與參數(shù)方程選講
以坐標原點
為極點，以
軸正半軸為極軸，建立極坐標系，
在直角坐標系
中，曲線
的參數(shù)方程為
（
是參數(shù)， 
），以原點
為極點， 
軸正半軸為極軸建立極坐標系，曲線
的極坐標方程為
.
（1）求曲線
的普通方程和曲線
的直角坐標方程；
（2）當
時，曲線
和
相交于
、
兩點，求以線段
為直徑的圓的直角坐標方程.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
