
【題目】已知函數![]() ,其中
,其中![]() ,
,![]() ,
,![]() 為自然對數的底數.
為自然對數的底數.
![]() 若
若![]() ,
,![]() ,①若函數
,①若函數![]() 單調遞增,求實數
單調遞增,求實數![]() 的取值范圍;②若對任意
的取值范圍;②若對任意![]() ,
,![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍.
的取值范圍.
![]() 若
若![]() ,且
,且![]() 存在兩個極值點
存在兩個極值點![]() ,
,![]() ,求證:
,求證:![]() .
.
【答案】![]() ①
①![]() ;②
;②![]() ;
;![]() 證明見解析.
證明見解析.
【解析】
![]() ①問題等價于
①問題等價于![]() 在
在![]() 上恒成立,即
上恒成立,即![]() 對任意
對任意![]() 恒成立,由此得解;②分
恒成立,由此得解;②分![]() 及
及![]() 討論,容易得出結論;
討論,容易得出結論;
![]() 解法一:表示出
解法一:表示出![]() ,令
,令![]() ,求導后易證
,求導后易證![]() ;令
;令![]() ,
,![]() ,利用導數可證
,利用導數可證![]() ,進而得證
,進而得證![]() ;解法二:不等式的右邊同解法一;由
;解法二:不等式的右邊同解法一;由![]() 當
當![]() 時,可得
時,可得![]() ,由此得出
,由此得出![]()
![]()
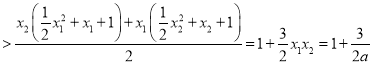 ,可得證.
,可得證.
解:![]() ①因為
①因為![]() 單調遞增,所以
單調遞增,所以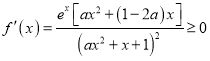 對任意
對任意![]() 恒成立,即
恒成立,即![]() 對任意
對任意![]() 恒成立,
恒成立,
![]() ,即
,即![]() ;
;
②由①當![]() 時,
時,![]() 單調遞增,故
單調遞增,故![]() 成立,符合題意,
成立,符合題意,
當![]() 時,令
時,令![]() 得
得![]() ,
,
![]()
![]() 在
在![]() 上遞減,
上遞減,![]()
![]() 不合題意;
不合題意;
綜上,實數![]() 的取值范圍為
的取值范圍為![]() .
.
![]() 解法一:因為
解法一:因為![]() ,
,![]() 存在兩個極值點
存在兩個極值點![]() ,
,![]() ,
,
所以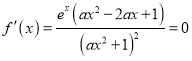 有兩個不同的解,故
有兩個不同的解,故![]() ,又
,又![]() ,所以
,所以![]() ,
,
設兩根為![]() ,
,![]()
![]() ,則
,則![]() ,
,![]() ,故
,故![]() ,
,
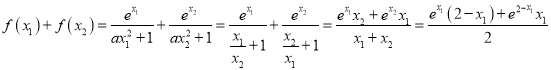
令![]() ,因為
,因為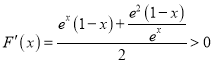 ,所以
,所以![]() 在
在![]() 上遞增,所以
上遞增,所以![]() ;
;
又![]()
令![]() ,
,![]() ,則
,則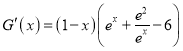 ,
,
令![]() 得
得![]() ,又
,又![]() ,則
,則![]() ,
,
即![]() ,記為
,記為![]() ,則
,則![]() 在
在![]() 上遞增,在
上遞增,在![]() 上遞減,
上遞減,
又![]() ,
,![]() ,所以
,所以![]() ,即
,即![]() ,綜上:
,綜上:![]() .
.
解法二:不等式的右邊同解法一;
由![]() 當
當![]() 時,
時,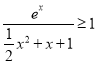 恒成立,所以有當
恒成立,所以有當![]() 時,
時,![]() ,所以
,所以
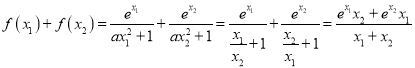
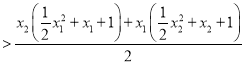
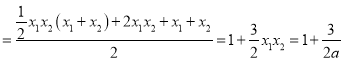 .
.


科目:高中數學 來源: 題型:
【題目】若關于x的不等式e2x﹣alnx![]() a恒成立,則實數a的取值范圍是( )
a恒成立,則實數a的取值范圍是( )
A.[0,2e]B.(﹣∞,2e]C.[0,2e2]D.(﹣∞,2e2]
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在極坐標系![]() 中,
中,![]() ,
,![]() ,弧
,弧![]() ,
,![]() ,
,![]() 所在圓的圓心分別為
所在圓的圓心分別為![]() ,
,![]() ,
,![]() ,曲線
,曲線![]() 是弧
是弧![]() ,曲線
,曲線![]() 是弧
是弧![]() ,曲線
,曲線![]() 是弧
是弧![]() .
.
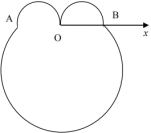
(1)寫出曲線![]() ,
,![]() ,
,![]() 的極坐標方程;
的極坐標方程;
(2)曲線![]() 由
由![]() ,
,![]() ,
,![]() 構成,若曲線
構成,若曲線![]() 的極坐標方程為
的極坐標方程為![]() (
(![]() ,
,![]() ,
,![]() ,
,![]() ),寫出曲線
),寫出曲線![]() 與曲線
與曲線![]() 的所有公共點(除極點外)的極坐標.
的所有公共點(除極點外)的極坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() 滿足奇數項
滿足奇數項![]() 成等差,公差為
成等差,公差為![]() ,偶數項
,偶數項![]() 成等比,公比為
成等比,公比為![]() ,且數列
,且數列![]() 的前
的前![]() 項和為
項和為![]() ,
,![]() ,
,![]() .
.
![]() 若
若![]() ,
,![]() .
.
①求數列![]() 的通項公式;
的通項公式;
②若![]() ,求正整數
,求正整數![]() 的值;
的值;
![]() 若
若![]() ,
,![]() ,對任意給定的
,對任意給定的![]() ,是否存在實數
,是否存在實數![]() ,使得
,使得![]() 對任意
對任意![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的取值范圍;若不存在,請說明理由.
的取值范圍;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】全民健身旨在全面提高國民體質和健康水平,倡導全民做到每天參加一次以上的健身活動,學會兩種以上健身方法,每年進行一次體質測定.為響應全民健身號召,某單位在職工體測后就某項健康指數(百分制)隨機抽取了30名職工的體測數據作為樣本進行調查,具體數據如莖葉圖所示,其中有1名女職工的健康指數的數據模糊不清(用x表示),已知這30名職工的健康指數的平均數為76.2.
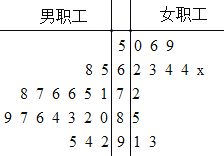
(1)根據莖葉圖,求樣本中男職工健康指數的眾數和中位數;
(2)根據莖葉圖,按男女用分層抽樣從這30名職工中隨機抽取5人,再從抽取的5人中隨機抽取2人,求抽取的2人都是男職工的概率;
(3)經計算,樣本中男職工健康指數的平均數為81,女職工現有數據(即剔除x)健康指數的平均數為69,方差為190,求樣本中所有女職工的健康指數的平均數和方差(結果精確到0.1).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若函數![]() (M>0,
(M>0,![]() >0,0<
>0,0<![]() <
<![]() )的最小值是﹣2,最小正周期是2
)的最小值是﹣2,最小正周期是2![]() ,且圖象經過點N(
,且圖象經過點N(![]() ,1).
,1).
(1)求![]() 的解析式;
的解析式;
(2)在△ABC中,若![]() ,
,![]() ,求cosC的值.
,求cosC的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com