
【題目】已知函數![]() ,
,![]() .
.
(1)若函數![]() 在其定義域上為單調增函數,求
在其定義域上為單調增函數,求![]() 的取值范圍;
的取值范圍;
(2)記![]() 的導函數為
的導函數為![]() ,當
,當![]() 時,證明:
時,證明:![]() 存在極小值點
存在極小值點![]() ,且
,且![]() .
.
【答案】(1)![]() (2)見解析
(2)見解析
【解析】分析:(1)函數![]() 在
在![]() 上為單調增函數,等價于
上為單調增函數,等價于![]() 對任意
對任意![]() 恒成立,
恒成立,![]() 對任意
對任意![]() 恒成立,只需
恒成立,只需![]() ,
,![]() ,利用導數研究函數的單調性,利用單調性求出函數最大值,從而可得結果;(2)由(1)得
,利用導數研究函數的單調性,利用單調性求出函數最大值,從而可得結果;(2)由(1)得![]() ,其中
,其中![]() ,
,![]() ,
,![]() ,
,
∵![]() ,∴
,∴![]() 與
與![]() 同號,令
同號,令![]() ,
,![]() ,存在
,存在![]() ,使得
,使得![]() ,
,![]() 是
是![]() 的極小值點,
的極小值點,![]() .
.
詳解:(1)依題意函數![]() 的定義域為
的定義域為![]() 且函數
且函數![]() 在
在![]() 上為單調增函數,
上為單調增函數,
所以![]()
![]() 對任意
對任意![]() 恒成立,
恒成立,
∴![]() 對任意
對任意![]() 恒成立,
恒成立,
∴![]() 對任意
對任意![]() 恒成立,
恒成立,
∴![]() ,
,![]() ,
,
令![]() ,
,![]() ,
,
∴![]() ,
,
∴當![]() 時,
時,![]() ,
,![]() 為增函數;當
為增函數;當![]() 時,
時,![]() ,
,![]() 為減函數,
為減函數,
∴當![]() 時,
時,![]() ,
,
∴![]() ,即
,即![]() 的取值范圍是
的取值范圍是![]() .
.
(2)由(1)得![]() ,其中
,其中![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,∴
,∴![]() 與
與![]() 同號,
同號,
令![]() ,
,![]() ,
,
∴![]()
![]() ,
,
∴當![]() 時,
時,![]() ,即函數
,即函數![]() 在
在![]() 上單調遞增,
上單調遞增,
∵![]() ,∴
,∴![]() ,
,![]() ,
,
∴存在![]() ,使得
,使得![]() ,
,
∴當![]() 時,
時,![]() ,
,![]() ,
,![]() 是減函數,
是減函數,
∴當![]() 時,
時,![]() ,
,![]() ,
,![]() 是增函數,
是增函數,
∴當![]() 時,存在
時,存在![]() ,使
,使![]() 是
是![]() 的極小值點.
的極小值點.
又由![]() 得
得![]() ,
,
所以![]() ,
,![]() ,
,
所以![]() .
.


科目:高中數學 來源: 題型:
【題目】某校200名學生的數學期中考試成績頻率分布直方圖如圖所示,其中成績分組區間是![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.

(1)求圖中![]() 的值;
的值;
(2)根據頻率分布直方圖,估計這200名學生的平均分;
(3)若這200名學生的數學成績中,某些分數段的人數![]() 與英語成績相應分數段的人數
與英語成績相應分數段的人數![]() 之比如下表所示,求英語成績在
之比如下表所示,求英語成績在![]() 的人數.
的人數.
分數段 |
|
|
|
|
|
| 1:2 | 2:1 | 6:5 | 1:2 | 1:1 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠新研發了一種產品,該產品每件成本為5元,將該產品按事先擬定的價格進行銷售,得到如下數據:
單價 | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
銷量 | 90 | 84 | 83 | 80 | 75 | 68 |
(1)求銷量![]() (件)關于單價
(件)關于單價![]() (元)的線性回歸方程
(元)的線性回歸方程![]() ;
;
(2)若單價定為10元,估計銷量為多少件;
(3)根據銷量![]() 關于單價
關于單價![]() 的線性回歸方程,要使利潤
的線性回歸方程,要使利潤![]() 最大,應將價格定為多少?
最大,應將價格定為多少?
參考公式: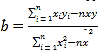 ,
,![]() .參考數據:
.參考數據:![]() ,
,![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某單位共有老、中、青職工430人,其中青年職工160人,中年職工人數是老年職工人數的2倍。為了解職工身體狀況,現采用分層抽樣方法進行調查,在抽取的樣本中有青年職工32人,則該樣本中的老年職工人數為
A. 9 B. 18 C. 27 D. 36
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知定義在(0,+∞)上的連續函數y=f(x)滿足:xf′(x)﹣f(x)=xex且f(1)=﹣3,f(2)=0.則函數y=f(x)( )
A.有極小值,無極大值
B.有極大值,無極小值
C.既有極小值又有極大值
D.既無極小值又無極大值
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】小王每天自己開車上班,他在路上所用的時間![]() (分鐘)與道路的擁堵情況有關.小王在一年中隨機記錄了200次上班在路上所用的時間,其頻數統計如下表,用頻率近似代替概率.
(分鐘)與道路的擁堵情況有關.小王在一年中隨機記錄了200次上班在路上所用的時間,其頻數統計如下表,用頻率近似代替概率.
| 15 | 20 | 25 | 30 |
頻數(次) | 50 | 50 | 60 | 40 |
(Ⅰ)求小王上班在路上所用時間的數學期望![]() ;
;
(Ⅱ)若小王一周上班5天,每天的道路擁堵情況彼此獨立,設一周內上班在路上所用時間不超過![]() 的天數為
的天數為![]() ,求
,求![]() 的分布列及數學期望.
的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知A(x0 , 0),B(0,y0)兩點分別在x軸和y軸上運動,且|AB|=1,若動點P(x,y)滿足 ![]() .
.
(1)求出動點P的軌跡對應曲線C的標準方程;
(2)一條縱截距為2的直線l1與曲線C交于P,Q兩點,若以PQ直徑的圓恰過原點,求出直線方程;
(3)直線l2:x=ty+1與曲線C交于A、B兩點,E(1,0),試問:當t變化時,是否存在一直線l2 , 使△ABE的面積為 ![]() ?若存在,求出直線l2的方程;若不存在,說明理由.
?若存在,求出直線l2的方程;若不存在,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com