
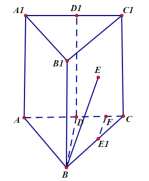
【題目】如圖,正三棱柱![]() 中,
中,![]() 、點
、點![]() 為
為![]() 中點,點
中點,點![]() 為四邊形
為四邊形![]() 內(包含邊界)的動點則以下結論正確的是( )
內(包含邊界)的動點則以下結論正確的是( )

A.![]()
B.若![]() 平面
平面![]() ,則動點
,則動點![]() 的軌跡的長度等于
的軌跡的長度等于![]()
![]()
C.異面直線![]() 與
與![]() ,所成角的余弦值為
,所成角的余弦值為![]()
D.若點![]() 到平面
到平面![]() 的距離等于
的距離等于![]() ,則動點
,則動點![]() 的軌跡為拋物線的一部分
的軌跡為拋物線的一部分
【答案】BCD
【解析】
根據空間向量的加減法運算以及通過建立空間直角坐標系求解,逐項判斷,進而可得到本題答案.
解析:對于選項A,![]() ,選項A錯誤;
,選項A錯誤;
對于選項B,過點![]() 作
作![]() 的平行線交
的平行線交![]() 于點
于點![]() .
.
以![]() 為坐標原點,
為坐標原點,![]() 分別為
分別為![]() 軸的正方向建立空間直角坐標系
軸的正方向建立空間直角坐標系![]() .
.
設棱柱底面邊長為![]() ,側棱長為
,側棱長為![]() ,則
,則![]() ,
,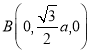 ,
,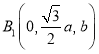 ,
,![]() ,所以
,所以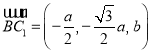 ,
,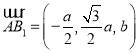 .
.
∵![]() ,∴
,∴![]() ,
,
即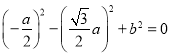 ,解得
,解得![]() .
.
因為![]() 平面
平面![]() ,則動點
,則動點![]() 的軌跡的長度等于
的軌跡的長度等于![]() .選項B正確.
.選項B正確.
對于選項C,在選項A的基礎上,![]() ,
,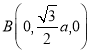 ,
,![]() ,
,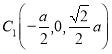 ,所以
,所以![]() ,
,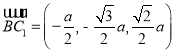 ,
,
因為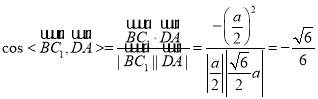 ,所以異面直線
,所以異面直線![]() 所成角的余弦值為
所成角的余弦值為![]() ,選項C正確.
,選項C正確.
對于選項D,設點E在底面ABC的射影為![]() ,作
,作![]() 垂直于
垂直于![]() ,垂足為F,若點E到平面
,垂足為F,若點E到平面![]() 的距離等于
的距離等于![]() ,即有
,即有![]() ,又因為在
,又因為在![]() 中,
中,![]() ,得
,得![]() ,其中
,其中![]() 等于點E到直線
等于點E到直線![]() 的距離,故點E滿足拋物線的定義,另外點E為四邊形
的距離,故點E滿足拋物線的定義,另外點E為四邊形![]() 內(包含邊界)的動點,所以動點E的軌跡為拋物線的一部分,故D正確.
內(包含邊界)的動點,所以動點E的軌跡為拋物線的一部分,故D正確.
故選:BCD


科目:高中數學 來源: 題型:
【題目】隨著城市地鐵建設的持續推進,市民的出行也越來越便利.根據大數據統計,某條地鐵線路運行時,發車時間間隔t(單位:分鐘)滿足:4≤t≤15,![]() N,平均每趟地鐵的載客人數p(t)(單位:人)與發車時間間隔t近似地滿足下列函數關系:
N,平均每趟地鐵的載客人數p(t)(單位:人)與發車時間間隔t近似地滿足下列函數關系: ,其中
,其中![]() .
.
(1)若平均每趟地鐵的載客人數不超過1500人,試求發車時間間隔t的值.
(2)若平均每趟地鐵每分鐘的凈收益為![]() (單位:元),問當發車時間間隔t為多少時,平均每趟地鐵每分鐘的凈收益最大?井求出最大凈收益.
(單位:元),問當發車時間間隔t為多少時,平均每趟地鐵每分鐘的凈收益最大?井求出最大凈收益.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某地區有小學21所,中學14所,大學7所.現采用分層抽樣的方法從這些學校中抽取6所學校,對學生進行視力檢查.
(Ⅰ) 求應從小學、中學、大學中分別抽取的學校數目;
(Ⅱ) 若從抽取的6所學校中隨即抽取2所學校作進一步數據
①列出所有可能抽取的結果;
②求抽取的2所學校沒有大學的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一年之計在于春,一日之計在于晨,春天是播種的季節,是希望的開端.某種植戶對一塊地的![]() 個坑進行播種,每個坑播3粒種子,每粒種子發芽的概率均為
個坑進行播種,每個坑播3粒種子,每粒種子發芽的概率均為![]() ,且每粒種子是否發芽相互獨立.對每一個坑而言,如果至少有兩粒種子發芽,則不需要進行補播種,否則要補播種.
,且每粒種子是否發芽相互獨立.對每一個坑而言,如果至少有兩粒種子發芽,則不需要進行補播種,否則要補播種.
(1)當![]() 取何值時,有3個坑要補播種的概率最大?最大概率為多少?
取何值時,有3個坑要補播種的概率最大?最大概率為多少?
(2)當![]() 時,用
時,用![]() 表示要補播種的坑的個數,求
表示要補播種的坑的個數,求![]() 的分布列與數學期望.
的分布列與數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給出下列三個命題:(1)如果一個平面內有無數條直線平行于另一個平面,則這兩個平面平行;(2)一個平面內的任意一條直線都與另一個平面不相交,則這兩個平面平行;(3)一個平面內有不共線的三點到另一個平面的距離相等,則這兩個平面平行;其中正確命題的個數是( )
A. 0B. 1C. 2D. 3
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]()
![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,
,![]() ,橢圓
,橢圓![]() 的長軸長與焦距之比為
的長軸長與焦距之比為![]() ,過
,過![]() 的直線
的直線![]() 與
與![]() 交于
交于![]() ,
,![]() 兩點.
兩點.
(1)當![]() 的斜率為
的斜率為![]() 時,求
時,求![]() 的面積;
的面積;
(2)當線段![]() 的垂直平分線在
的垂直平分線在![]() 軸上的截距最小時,求直線
軸上的截距最小時,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了檢測某種零件的一條生產線的生產過程,從生產線上隨機抽取一批零件,根據其尺寸的數據得到如圖所示的頻率分布直方圖.若尺寸落在區間(![]() )之外,則認為該零件屬“不合格”的零件,其中
)之外,則認為該零件屬“不合格”的零件,其中![]() ,分別為樣本平均數和樣本標準差,計算可得:
,分別為樣本平均數和樣本標準差,計算可得:![]() (同一組中的數據用該組區間的中點值作代表).
(同一組中的數據用該組區間的中點值作代表).

(1)若一個零件的尺寸是![]() ,試判斷該零件是否屬于“不合格”的零件;
,試判斷該零件是否屬于“不合格”的零件;
(2)工廠利用分層抽樣的方法從樣本的前3組中抽出6個零件,標上記號,并從這6個零件中再抽取2個,求再次抽取的2個零件中恰有1個尺寸不超過![]() 的概率.
的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,把函數
,把函數![]() 的圖象向右平移
的圖象向右平移![]() 個單位,再把圖象上各點的橫坐標縮小到原來的一半,縱坐標不變,得到函數
個單位,再把圖象上各點的橫坐標縮小到原來的一半,縱坐標不變,得到函數![]() 的圖象,當
的圖象,當![]() 時,方程
時,方程![]() 恰有兩個不同的實根,則實數
恰有兩個不同的實根,則實數![]() 的取值范圍為( )
的取值范圍為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面ABCD為矩形,O,E分別為AD,PB的中點,平面
中,底面ABCD為矩形,O,E分別為AD,PB的中點,平面![]() 平面ABCD,
平面ABCD,![]() ,
,![]() .
.
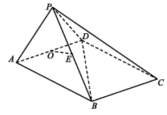
(1)求證:![]() 平面PCD;
平面PCD;
(2)求證:![]() 平面PCD;
平面PCD;
(3)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com