【題目】已知
汽車站每天上午
，
之間都恰有一輛長途汽車經過，但是長途車到站的時間是隨機的，且每輛車的到站時間是相互獨立的，汽車到站后即停即走，據統計汽車到站規律為：
現有一位旅客在
到達汽車站，問：
（1）該旅客候車時間不超過20分鐘的概率；
（2）記該旅客的候車時間為
，求的概率分布列及數學期望．
金博士一點全通系列答案科目：高中數學 來源： 題型：
【題目】從分別寫有1,2,3,4,5的5張卡片中隨機抽取1張，放回后再隨機抽取1張，則抽得的第一張卡片上的數大于第二張卡片上的數的概率為( )
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】分形理論是當今世界十分風靡和活躍的新理論、新學科。其中，把部分與整體以某種方式相似的形體稱為分形。分形是一種具有自相似特性的現象，圖象或者物理過程。標準的自相似分形是數學上的抽象，迭代生成無限精細的結構。也就是說，在分形中，每一組成部分都在特征上和整體相似，只僅僅是變小了一些而已，謝爾賓斯基三角形就是一種典型的分形，是由波蘭數學家謝爾賓斯基在1915年提出的，按照如下規律依次在一個黑色三角形內去掉小三角形則當
時，該黑色三角形內共去掉( )個小三角形
A. 81 B. 121 C. 364 D. 1093
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知一個三棱錐的三視圖如圖所示，其中俯視圖是頂角為
的等腰三角形，側視圖為直
角三角形，則該三棱錐的表面積為____，該三棱錐的外接球體積為____．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】“微信運動”已經成為當下熱門的健身方式，韓梅梅的微信朋友圈內有800為好友參與了“微信運動”.他隨機抽取了50為微信好友（男、女各25人），統計其在某一天的走路步數.其中女性好友的走路步數數據記錄如下：
12860 8320 10231 6734 7323 8430 3200 4543 11123 9860
8753 6454 7292 4850 10222 9734 7944 9117 6421 2980
1123 1786 2436 3876 4326
男性好友走路步數情況可以分為五個類別
（0-2000步）（說明：“0-2000”表示大于等于0，小于等于2000，下同），
（2001-5000）、
（5001-8000）、
（8001-10000步）、
（10001步及以上），且
三中類型的人數比例為
，將統計結果繪制如圖所示的柱形圖.
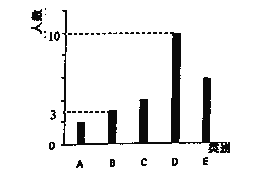
若某人一天的走路步數超過8000步則被系統評定為“積極型”，否則被系統評定為“懈怠型”.
（1）若以韓梅梅抽取的好友當天行走步數的頻率分布來估計所有微信好友每日走路步數的概率分布，請估計韓梅梅的微信好友圈里參與“微信運動”的800名好友中，每天走路步數在5001-10000步的人數；
（2）請根據選取的樣本數據完成下面的
列聯表，并據此判斷能否有95%以上的把握認為“評定類型”與“性別”有關？
積極型 | 懈怠型 | 總計 | |
男 | 25 | ||
女 | 25 | ||
總計 | 30 |
（3）若從韓梅梅當天選取的步數大于10000的好友中按男女比例分層選取5人進行身體狀況調查，然后再從這5位好友中選取2人進行訪談，求至少有一位女性好友訪談的概率.
參考公式：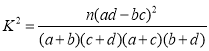
，其中
.
臨界值表：
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】有下列說法：
①若某商品的銷售量
（件）關于銷售價格
（元/件）的線性回歸方程為
，當銷售價格為10元時，銷售量一定為300件；
②線性回歸直線
一定過樣本點中心
；
③若兩個隨機變量的線性相關性越強，則相關系數
的值越接近于1；
④在殘差圖中，殘差點比較均勻落在水平的帶狀區域中即可說明選用的模型比較合適，與帶狀區域的寬度無關；
⑤在線性回歸模型中，相關指數
表示解釋變量對于預報變量變化的貢獻率，越接近于1，表示回歸的效果越好；
其中正確的結論有幾個（ ）
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】
11分制乒乓球比賽，每贏一球得1分，當某局打成10:10平后，每球交換發球權，先多得2分的一方獲勝，該局比賽結束.甲、乙兩位同學進行單打比賽，假設甲發球時甲得分的概率為0.5，乙發球時甲得分的概率為0.4，各球的結果相互獨立.在某局雙方10:10平后，甲先發球，兩人又打了X個球該局比賽結束.
（1）求P（X=2）；
（2）求事件“X=4且甲獲勝”的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】2022年北京冬奧會的申辦成功與“3億人上冰雪”口號的提出，將冰雪這個冷項目迅速炒“熱”．北京某綜合大學計劃在一年級開設冰球課程，為了解學生對冰球運動的興趣，隨機從該校一年級學生中抽取了100人進行調查，其中女生中對冰球運動有興趣的占
，而男生有10人表示對冰球運動沒有興趣額．
（1）完成
列聯表，并回答能否有
的把握認為“對冰球是否有興趣與性別有關”？
有興趣 | 沒興趣 | 合計 | |
男 | 55 | ||
女 | |||
合計 |
（2）若將頻率視為概率，現再從該校一年級全體學生中，采用隨機抽樣的方法每次抽取1名學生，抽取5次，記被抽取的5名學生中對冰球有興趣的人數為
，若每次抽取的結果是相互獨立的，求的分布列，期望和方差．
附表：
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
