
【題目】數列![]() 是首項與公比均為
是首項與公比均為![]() 的等比數列(
的等比數列(![]() ,且
,且![]() ),數列
),數列![]() 滿足
滿足![]() .
.
(1)求數列![]() 的前
的前![]() 項和
項和![]() ;
;
(2)若對一切![]() 都有
都有![]() ,求
,求![]() 的取值范圍.
的取值范圍.
【答案】(1)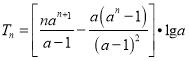 ;(2)
;(2)![]() 或
或![]() .
.
【解析】試題分析:(1)先求出數列![]() 的通項公式,從而可得
的通項公式,從而可得![]() ,利用錯位相減法求解即可;(2)由
,利用錯位相減法求解即可;(2)由![]() 得
得![]() ,討論
,討論![]() 時,
時, ![]() 時兩種情況,分別分離參數,求出
時兩種情況,分別分離參數,求出![]() 的最值,即可求
的最值,即可求![]() 的取值范圍.
的取值范圍.
試題解析:(1)∵數列![]() 是首項為
是首項為![]() ,公比為
,公比為![]() 的等比數列.
的等比數列.
∴![]() .
.
從而![]() ,∴
,∴![]()
![]() .
.
設![]() ,則
,則![]() ,
,
∴![]()
![]() ,
,
∴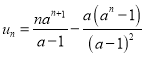 ,∴
,∴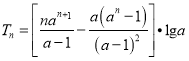 .
.
(2)由![]() 得
得![]() .
.
①當![]() 時,
時, ![]() ,可得
,可得![]() ,
,
∵![]() ,
, ![]() ,
,
∴![]() 對一切
對一切![]() 都成立,此時的解為
都成立,此時的解為![]() ;
;
②當![]() 時,
時, ![]() ,可得
,可得![]() ,
,
∵![]() ,
, ![]() ,
,
∴![]() 對一切
對一切![]() 都成立時
都成立時![]() .
.
由①,②可知,對一切![]() 都有
都有![]() 的
的![]() 的取值范圍是
的取值范圍是![]() 或
或![]() .
.
【易錯點晴】本題主要考察等差數列的通項公式、等比數列的求和公式、“錯位相減法”求數列的和,以及不等式恒成立問題,屬于難題. “錯位相減法”求數列的和是重點也是難點,利用“錯位相減法”求數列的和應注意以下幾點:①掌握運用“錯位相減法”求數列的和的條件(一個等差數列與一個等比數列的積);②相減時注意最后一項 的符號;③求和時注意項數別出錯;④最后結果一定不能忘記等式兩邊同時除以![]() .
.


科目:高中數學 來源: 題型:
【題目】近年來,我國“霧霾天氣”頻發,嚴重影響人們的身體健康.根據空氣質量指數API(為整數)的不同,可將空氣質量分級如下表:
API | 0~50 | 51~100 | 101~150 | 151~200 | 201~250 | 251~300 | >300 |
級別 | Ⅰ | Ⅱ | Ⅲ1 | Ⅲ2 | Ⅳ1 | Ⅳ2 | Ⅴ |
狀況 | 優 | 良 | 輕微污染 | 輕度污染 | 中度污染 | 中度重污染 | 重度污染 |
|
|
|
|
| |||
對某城市一年(365天)的空氣質量進行監測,獲得的API數據按照區間[0,50],(50,100],(100,150],(150,200],(200,250],(250,300]進行分組,得到頻率分布直方圖如圖.
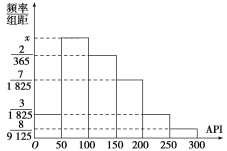
(1)求頻率分布直方圖中x的值;
(2)計算一年中空氣質量分別為良和輕微污染的天數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】今有一組數據如下表:
| 1 | 2 | 3 | 4 | 5 | 6 |
| 4 | 5 | 6 | 7 | 8 | 9 |
| 90 | 84 | 83 | m | 75 | 68 |
由最小二乘法求得點![]()
![]() 的回歸直線方程是
的回歸直線方程是![]() ,其中
,其中![]() .
.
(Ⅰ)求m的值,并求回歸直線方程;
(Ⅱ)設![]() ,我們稱
,我們稱![]() 為點
為點![]() 的殘差,記為
的殘差,記為![]() .
.
從所給的點![]()
![]() 中任取兩個,求其中有且只有一個點的殘差絕對值不大于1的概率.
中任取兩個,求其中有且只有一個點的殘差絕對值不大于1的概率.
參考公式:  .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]()
![]() 的長軸長是短軸長的2倍,且過點
的長軸長是短軸長的2倍,且過點![]() .
.
⑴求橢圓![]() 的方程;
的方程;
⑵若在橢圓上有相異的兩點![]() (
(![]() 三點不共線),
三點不共線),![]() 為坐標原點,且直線
為坐標原點,且直線![]() ,直線
,直線![]() ,直線
,直線![]() 的斜率滿足
的斜率滿足![]() .
.
(ⅰ)求證: ![]() 是定值;
是定值;
(ⅱ)設![]() 的面積為
的面積為![]() ,當
,當![]() 取得最大值時,求直線
取得最大值時,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】袋子里有編號為![]() 的五個球,某位教師從袋中任取兩個不同的球. 教師把所取兩球編號的和只告訴甲,其乘積只告訴乙,讓甲、乙分別推斷這兩個球的編號.
的五個球,某位教師從袋中任取兩個不同的球. 教師把所取兩球編號的和只告訴甲,其乘積只告訴乙,讓甲、乙分別推斷這兩個球的編號.
甲說:“我無法確定.”
乙說:“我也無法確定.”
甲聽完乙的回答以后,甲又說:“我可以確定了.”
根據以上信息, 你可以推斷出抽取的兩球中
A. 一定有3號球 B. 一定沒有3號球 C. 可能有5號球 D. 可能有6號球
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() ,點
,點![]() ,點
,點![]() 是圓上任意一點,線段
是圓上任意一點,線段![]() 的垂直平分線交
的垂直平分線交![]() 于點
于點![]() ,設動點
,設動點![]() 的軌跡為
的軌跡為![]() .
.
(Ⅰ)求![]() 的方程;
的方程;
(Ⅱ)設直線![]() 與軌跡
與軌跡![]() 交于
交于![]() 兩點,
兩點, ![]() 為坐標原點,若
為坐標原點,若![]() 的重心恰好在圓
的重心恰好在圓![]() 上,求
上,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com