
【題目】如圖, ![]() 平面
平面![]() 平面
平面![]() ,
, ![]() 是等邊三角形,
是等邊三角形, ![]() 是
是![]() 的中點.
的中點.

(1)證明: ![]() ;
;
(2)若直線![]() 與平面
與平面![]() 所成角的余弦值為
所成角的余弦值為![]() ,求二面角
,求二面角![]() 的正弦值.
的正弦值.
【答案】(1)證明見解析;(2)![]() .
.
【解析】試題分析:(1)由![]() 是等邊三角形,
是等邊三角形, ![]() 是
是![]() 的中點,可得
的中點,可得![]() ,利用直線與平面垂直的判定定理得出直線與平面垂直,再利用直線與平面垂直的性質定理證明線線垂直;(2)以點
,利用直線與平面垂直的判定定理得出直線與平面垂直,再利用直線與平面垂直的性質定理證明線線垂直;(2)以點![]() 為坐標原點,
為坐標原點, ![]() 所在直線為
所在直線為![]() 軸,
軸, ![]() 所在直線為
所在直線為![]() 軸,過
軸,過![]() 且與直線
且與直線![]() 平的直線為
平的直線為![]() 軸,建立空間直角坐標系,根據直線
軸,建立空間直角坐標系,根據直線![]() 與平面
與平面![]() 所成的角的余弦值為
所成的角的余弦值為![]() .可得
.可得![]() ,不妨設
,不妨設![]() ,利用向量垂直數量積為零,分別求出平面
,利用向量垂直數量積為零,分別求出平面![]() 與平面
與平面![]() 的法向量,利用空間向量夾角余弦公式可得二面角
的法向量,利用空間向量夾角余弦公式可得二面角![]() 的余弦值,進而可得正弦值.
的余弦值,進而可得正弦值.
試題解析:(1)因為![]() 是等邊三角形,
是等邊三角形, ![]() 是
是![]() 的中點,所以
的中點,所以![]() ,因為
,因為![]() 平面
平面![]() 平面
平面![]() ,所以
,所以![]() ,因為
,因為![]() ,所以
,所以![]() 平面
平面![]() ,因為
,因為![]() 平面
平面![]() ,所以
,所以![]() .
.
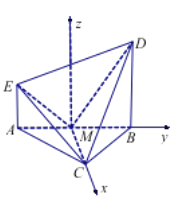
(2)解法1: 以點![]() 為坐標原點,
為坐標原點, ![]() 所在直線為
所在直線為![]() 軸,
軸, ![]() 所在直線為
所在直線為![]() 軸,過
軸,過![]() 且與直線
且與直線![]() 平的直線為
平的直線為![]() 軸,建立如圖所示的空間直角坐標系
軸,建立如圖所示的空間直角坐標系![]() .
.
因為![]() 平面
平面![]() ,所以
,所以![]() 為直線
為直線![]() 與平面
與平面![]() 所成的角.
所成的角.
由題意得![]() ,
,![]() ,
,
即![]() ,從而
,從而![]() .不妨設
.不妨設![]() ,又
,又![]() ,則
,則![]() .
.
故![]() .
.
于是![]() ,
,
設平面![]() 與平面
與平面![]() 的法向量分別為
的法向量分別為![]() ,
,
由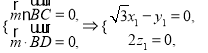 令
令![]() ,得
,得![]()
由 令
令![]() ,得
,得![]() .
.
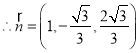 .
.
![]() .故二面角
.故二面角![]() 的正弦值為1.
的正弦值為1.
(2)解法2: ![]() 平面
平面![]() 為直線
為直線![]() 與平面
與平面![]() 所成的角.
所成的角.
由題意得![]() ,
,
即![]() ,從而
,從而![]() .
.
不妨設![]() ,又
,又![]() ,則
,則![]() ,
, ![]() .
.
由于![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,則
,則![]() .
.
取![]() 的中點
的中點![]() ,連接
,連接![]() ,則
,則![]() .
.
在![]() 中,
中, ![]() ,
,
在![]() 中,
中, ![]() ,
,
在![]() 中,
中, ![]() ,
,
取![]() 的中點
的中點![]() ,連接
,連接![]() ,則
,則![]() .
.
所以![]() 為二面角
為二面角![]() 的平面角.
的平面角.
在![]() 中,
中, ![]() ,
,
在![]() 中,
中, ![]() ,
,
在![]() 中,
中, ![]() ,
,
![]() .
.
故二面角![]() 的正弦值為1.
的正弦值為1.
【方法點晴】本題主要考查線面垂直的判定與性質,以及利用空間向量求二面角,屬于難題.空間向量解答立體幾何問題的一般步驟是:(1)觀察圖形,建立恰當的空間直角坐標系;(2)寫出相應點的坐標,求出相應直線的方向向量;(3)設出相應平面的法向量,利用兩直線垂直數量積為零列出方程組求出法向量;(4)將空間位置關系轉化為向量關系;(5)根據定理結論求出相應的角和距離.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】下列語句是否為命題?如果是,判斷它的真假.
(1)這道數學題有趣嗎?(2)0不可能不是自然數;(3)![]() ;(4)
;(4)![]() ;
;
(5)91不是素數;(6)上海的空氣質量越來越好.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“過大年,吃水餃”是我國不少地方過春節的一大習俗.2018年春節前夕, ![]() 市某質檢部門隨機抽取了100包某種品牌的速凍水餃,檢測其某項質量指標,檢測結果如頻率分布直方圖所示.
市某質檢部門隨機抽取了100包某種品牌的速凍水餃,檢測其某項質量指標,檢測結果如頻率分布直方圖所示.
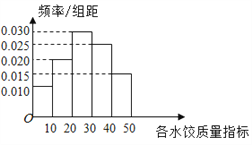
(1)求所抽取的100包速凍水餃該項質量指標值的樣本平均數![]() (同一組中數據用該組區間的中點值作代表);
(同一組中數據用該組區間的中點值作代表);
(2)①由直方圖可以認為,速凍水餃的該項質量指標值![]() 服從正態分布
服從正態分布![]() ,利用該正態分布,求
,利用該正態分布,求![]() 落在
落在![]() 內的概率;
內的概率;
②將頻率視為概率,若某人從某超市購買了4包這種品牌的速凍水餃,記這4包速凍水餃中這種質量指標值位于![]() 內的包數為
內的包數為![]() ,求
,求![]() 的分布列和數學期望.
的分布列和數學期望.
附:①計算得所抽查的這100包速凍水餃的質量指標的標準差為![]() ;
;
②若![]() ,則
,則![]() ,
, ![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com