【題目】已知函數(shù)
.
（1）討論
的單調區(qū)間；
（2）當
時，證明： 
.
【答案】（1）詳見解析；（2）詳見解析.
【解析】試題分析：（1）求函數(shù)的單調區(qū)間，先求導
，于導數(shù)可知導數(shù)的符號受參數(shù)
的取值的影響，根據(jù)
， 
， 
，分析即可，（2）要證
，問題轉化為
，然后構造函數(shù)
，只需證明
是增函數(shù)即可
試題解析：
解：（1）
的定義域為
，且
，
①當
時， 
，此時
的單調遞減區(qū)間為
.
②當
時，由
，得
；
由
，得
.
此時
的單調減區(qū)間為
，單調增區(qū)間為
.
③當
時，由
，得
；
由
，得
.
此時
的單調減區(qū)間為
，單調增區(qū)間為
.
（2）當
時，要證： 
，
只要證： 
，即證： 
.（*）
設
，則
，
設
，
由（1）知
在
上單調遞增，
所以當
時， 
，于是
，所以
在
上單調遞增，
所以當
時，（*）式成立，
故當
時， 
.
.
科目：高中數(shù)學 來源： 題型：
【題目】已知橢圓
：
的離心率為
，且過點
．
（Ⅰ）求橢圓的方程；
（Ⅱ）已知橢圓的左焦點為
，直線
與橢圓交于不同兩點
，
（
都在
軸上方），且
．
（ⅰ）若
，求
的面積；
（ⅱ）直線是否恒過定點？若過定點，求出該定點的坐標；若不過定點，請說明理由．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
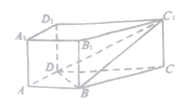
【題目】如圖，四棱柱
中，
底面
，底面是梯形，
，
，
.
（1）求證：平面
平面
；
（2）在線段
上是否存在一點
，使
平面，若存在，請確定點的位置；若不存在，請說明理由.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】2016年新高一學生入學后，為了了解新生學業(yè)水平，某區(qū)對新生進行了素質測查，隨機抽取了50名學生的數(shù)學成績（均低于100分），其相關數(shù)據(jù)統(tǒng)計如下：
分數(shù)段 | 頻數(shù) | 選擇題≥24分 |
| 5 | 2 |
| 10 | 4 |
| 15 | 12 |
| 10 | 6 |
| 5 | 4 |
| 5 | 5 |
（1）若全區(qū)高一新生有5000人，試估計成績不低于60分的人數(shù)；
（2）根據(jù)表格數(shù)據(jù)試估計全區(qū)新生數(shù)學的平均成績（同一分數(shù)段的數(shù)據(jù)取該區(qū)間的中點值作為代表，如區(qū)間
的中點值為75）；
（3）從成績在
中抽取選擇題得分不低于24分的3名學生進行具體分析，求至少有2名學生成績在
內的概率．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】函數(shù)y= 
﹣（x+1）0的定義域為（ ）
A.（﹣1， 
]
B.（﹣1， ）??
C.（﹣∞，﹣1）∪（﹣1， ]
D.[ ，+∞）
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知二次函數(shù)f（x）=ax2+bx+c（a≠0）的圖象過點（0，1）且與x軸有唯一的交點（﹣1，0）． （Ⅰ）求f（x）的表達式；
（Ⅱ）在（Ⅰ）的條件下，設函數(shù)F（x）=f（x）﹣mx，若F（x）在區(qū)間[﹣2，2]上是單調函數(shù)，求實數(shù)m的取值范圍；
（Ⅲ）設函數(shù)g（x）=f（x）﹣kx，x∈[﹣2，2]，記此函數(shù)的最小值為h（k），求h（k）的解析式．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】下表提供了某廠節(jié)油降耗技術發(fā)行后生產甲產品過程中記錄的產量 x (噸)與相應的生產能耗y(噸標準煤)的幾組對應數(shù)據(jù).
x | 3 | 4 | 5 | 6 |
y | 2.5 | 3 | 4 | 4.5 |
（1）請畫出上表數(shù)據(jù)的散點圖；
（2）請根據(jù)上表提供的數(shù)據(jù)，用最小二乘法求出 y 關于 x 的線性回歸方程
（3）已知該廠技改前 100 噸甲產品的生產能耗為 90 噸標準煤，試根據(jù)(2)求出的線性回歸方程，預測生產100 噸甲產品的生產能耗比技改前降低多少噸標準煤?(參考數(shù)值：3×2.5+4×3+5×4+6×4.5=66.5)
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知二次函數(shù)f（x）的最小值為1，且f（0）=f（2）=3．
（1）求f（x）的解析式；
（2）若f（x）在區(qū)間[2a，a+1]上不單調，求a的取值范圍
（3）若x∈[t，t+2]，試求y=f（x）的最小值．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
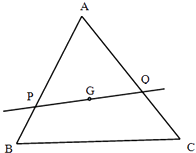
【題目】設G為△ABC的重心，過G作直線l分別交線段AB，AC（不與端點重合）于P，Q．若 
=λ 
， 
=μ 
． 
（1）求 
的值；
（2）求λμ的取值范圍．
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
