
【題目】(10分)設![]() 和
和![]() 分別是先后拋擲一枚骰子得到的點數(shù),用隨機變量
分別是先后拋擲一枚骰子得到的點數(shù),用隨機變量![]() 表示方程
表示方程
![]() 實根的個數(shù)(重根按一個計).
實根的個數(shù)(重根按一個計).
(Ⅰ)求方程![]() 有實根的概率;
有實根的概率;
(Ⅱ)求![]() 的分布列和數(shù)學期望;
的分布列和數(shù)學期望;
(Ⅲ)求在先后兩次出現(xiàn)的點數(shù)中有5的條件下,方程![]() 有實根的概率.
有實根的概率.
【答案】(Ⅰ)![]()
(Ⅱ)
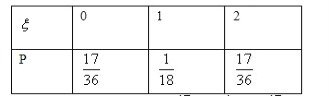
![]()
(Ⅲ)![]()
【解析】本試題主要考查了古典概型概率的計算,以及分布列和數(shù)學期望的求解的綜合運用。
(1)中理解本題是一個等可能事件的概率,試驗發(fā)生包含的基本事件總數(shù)為6×6=36,那么借助于使方程有實根△=b2-4c≥0,得到事件A發(fā)生的基本事件數(shù),得到概率值。
(2)利用ξ=0,1,2的可能取值,分別得到各個取值的概率值,然后寫出分布列和數(shù)學期望值
(3)分析在先后兩次出現(xiàn)的點數(shù)中有5的條件下,方程x2+bx+c=0有實根,這是一個條件概率,利用條件概率公式得到結(jié)論。
解:(I)由題意知,本題是一個等可能事件的概率,
試驗發(fā)生包含的基本事件總數(shù)為6×6=36,
滿足條件的事件是使方程有實根,則△=b2-4c≥0,即.
下面針對于c的取值進行討論
當c=1時,b=2,3,4,5,6; 當c=2時,b=3,4,5,6;
當c=3時,b=4,5,6; 當c=4時,b=4,5,6;
當c=5時,b=5,6; 當c=6時,b=5,6,
目標事件個數(shù)為5+4+3+3+2+2=19,
因此方程![]() 有實根的概率為
有實根的概率為![]()
(II)由題意知用隨機變量ξ表示方程![]() 實根的個數(shù)得到
實根的個數(shù)得到
ξ=0,1,2 根據(jù)第一問做出的結(jié)果得到
則![]() ,
,![]() ,
,![]() ,
,
∴ξ的分布列為

∴ξ的數(shù)學期望 ![]()
(III)在先后兩次出現(xiàn)的點數(shù)中有5的條件下,方程x2+bx+c=0有實根,
這是一個條件概率,
記“先后兩次出現(xiàn)的點數(shù)中有5”為事件M,
“方程![]() 有實根”為事件N,
有實根”為事件N,
則,![]() ,
,![]() ∴
∴![]()


 期末1卷素質(zhì)教育評估卷系列答案
期末1卷素質(zhì)教育評估卷系列答案科目:高中數(shù)學 來源: 題型:
【題目】試求下列函數(shù)的定義域與值域:
(1)f(x)=(x-1)2+1,x∈{-1,0,1,2,3};
(2)f(x)=(x-1)2+1;
(3)f(x)=![]() ;
;
(4)f(x)=x-![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知冪函數(shù)f(x)=x![]() (m∈N*).
(m∈N*).
(1)試確定該函數(shù)的定義域,并指明該函數(shù)在其定義域上的單調(diào)性;
(2)若該函數(shù)還經(jīng)過點(2, ![]() ),試確定m的值,并求滿足條件f(2-a)>f(a-1)的實數(shù)a的取值范圍.
),試確定m的值,并求滿足條件f(2-a)>f(a-1)的實數(shù)a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】2015男籃亞錦賽決賽階段,中國男籃以9連勝的不敗戰(zhàn)績贏得第28屆亞錦賽冠軍,同時拿到亞洲唯一1張直通里約奧運會的入場券,賽后,中國男籃主力易建聯(lián)榮膺本屆亞錦賽![]() (最有價值球員),下表是易建聯(lián)在這9場比賽中投籃的統(tǒng)計數(shù)據(jù).
(最有價值球員),下表是易建聯(lián)在這9場比賽中投籃的統(tǒng)計數(shù)據(jù).
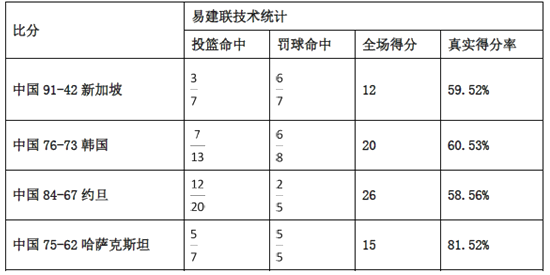
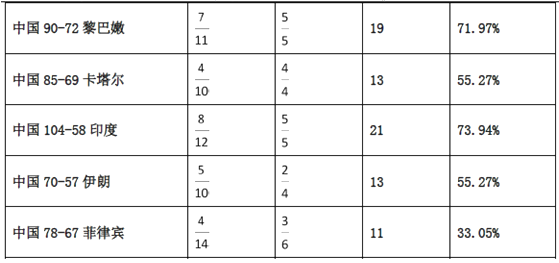
注:(1)表中![]() 表示出手
表示出手![]() 次命中
次命中![]() 次;
次;
(2)![]() (真實得分率)是衡量球員進攻的效率,其計算公式為:
(真實得分率)是衡量球員進攻的效率,其計算公式為:
![]()
![]()
(1)從上述9場比賽中隨機選擇一場,求易建聯(lián)在該場比賽中![]() 超過50%的概率;
超過50%的概率;
(2)從上述9場比賽中隨機選擇一場,求易建聯(lián)在該場比賽中![]() 至少有一場超過60%的概率;
至少有一場超過60%的概率;
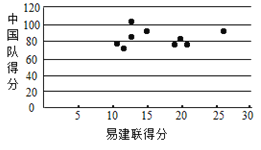
(3)用![]() 來表示易建聯(lián)某場的得分,用
來表示易建聯(lián)某場的得分,用![]() 來表示中國隊該場的總分,畫出散點圖如圖所示,請根據(jù)散點圖判斷
來表示中國隊該場的總分,畫出散點圖如圖所示,請根據(jù)散點圖判斷![]() 與
與![]() 之間是否具有線性相關關系?結(jié)合實際簡單說明理由.
之間是否具有線性相關關系?結(jié)合實際簡單說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() 是定義在區(qū)間
是定義在區(qū)間![]() 上的奇函數(shù),且
上的奇函數(shù),且![]() 若對于任意的
若對于任意的![]() 有
有![]()
(1)判斷并證明函數(shù)的單調(diào)性;
(2)解不等式![]() ;
;
(3)若![]() 對于任意的
對于任意的![]() ,
, ![]() 恒成立,求實數(shù)
恒成立,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)f(x)=x3+3x2-9x.
(I)求f(x)的單調(diào)區(qū)間;
(Ⅱ)若函數(shù)f(x)在區(qū)間[-4,c]上的最小值為-5,求c的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
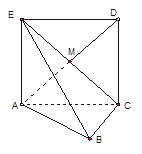
【題目】如圖,邊長為2的正方形ACDE所在的平面與平面ABC垂直,AD與CE的交點為M,![]() ,且AC=BC.
,且AC=BC.
(1)求證:![]() 平面EBC;
平面EBC;
(2)求二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某理科考生參加自主招生面試,從7道題中(4道理科題3道文科題)不放回地依次任取3道作答.
(1)求該考生在第一次抽到理科題的條件下,第二次和第三次均抽到文科題的概率;
(2)規(guī)定理科考生需作答兩道理科題和一道文科題,該考生答對理科題的概率均為![]() ,答對文科題的概率均為
,答對文科題的概率均為![]() ,若每題答對得10分,否則得零分.現(xiàn)該生已抽到三道題(兩理一文),求其所得總分
,若每題答對得10分,否則得零分.現(xiàn)該生已抽到三道題(兩理一文),求其所得總分![]() 的分布列與數(shù)學期望
的分布列與數(shù)學期望![]() .
.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com