
【題目】定義在![]() 上的函數
上的函數![]() ,如果滿足:對任意
,如果滿足:對任意![]() ,存在常數
,存在常數![]() ,都有
,都有![]() 成立,則稱
成立,則稱![]() 是
是![]() 上的有界函數,其中
上的有界函數,其中![]() 稱為函數
稱為函數![]() 的一個上界.已知函數
的一個上界.已知函數![]() ,
, ![]() .
.
(1)若函數![]() 為奇函數,求實數
為奇函數,求實數![]() 的值;
的值;
(2)在(1)的條件下,求函數![]() 在區間
在區間![]() 上的所有上界構成的集合;
上的所有上界構成的集合;
(3)若函數![]() 在
在![]() 上是以3為上界的有界函數,求實數
上是以3為上界的有界函數,求實數![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() ;(2)上界構成集合為
;(2)上界構成集合為![]() ;(3)實數
;(3)實數![]() 的取值范圍為
的取值范圍為![]() .
.
【解析】試題分析:(1)![]() ,即
,即![]() ,得
,得![]() ;(2)函數
;(2)函數![]() 在區間
在區間![]() 上單調遞增,所以值域為
上單調遞增,所以值域為![]() ,所以所有上界構成集合為
,所以所有上界構成集合為![]() ;(3)
;(3)![]() 在
在![]() 上恒成立,分離參數得
上恒成立,分離參數得![]() 在
在![]() 上恒成立,所以
上恒成立,所以![]() 的取值范圍為
的取值范圍為![]() .
.
試題解析:
(1)因為函數![]() 為奇函數,
為奇函數,
所以![]() ,即
,即![]() ,
,
即![]() ,得
,得![]() ,而當
,而當![]() 時不合題意,故
時不合題意,故![]() .
.
(2)由(1)得: ![]() ,
,
易知,函數![]() 在區間
在區間![]() 上單調遞增,
上單調遞增,
所以函數![]() 在區間
在區間![]() 上單調遞增,
上單調遞增,
所以函數![]() 在區間
在區間![]() 上的值域為
上的值域為![]() ,
,
所以![]() ,故函數
,故函數![]() 在區間
在區間![]() 上的所有上界構成集合為
上的所有上界構成集合為![]() .
.
(3)由題意知, ![]() 在
在![]() 上恒成立.
上恒成立.
![]() ,
, ![]() .
.
∴![]() 在
在![]() 上恒成立.
上恒成立.
∴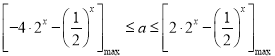
設![]() ,
, ![]() ,
, ![]() ,由
,由![]() 得
得![]() ,
,
設![]() ,
, ![]() ,
,
![]() ,
,
所以![]() 在
在![]() 上遞減,
上遞減, ![]() 在
在![]() 上遞增,
上遞增,
![]() 在
在![]() 上的最大值為
上的最大值為![]() ,
, ![]() 在
在![]() 上的最小值為
上的最小值為![]() .
.
所以實數![]() 的取值范圍為
的取值范圍為![]() .
.


 口算能手系列答案
口算能手系列答案科目:高中數學 來源: 題型:
【題目】正方形![]() 的棱長為1,點
的棱長為1,點![]() 分別是棱
分別是棱![]() 的中點.
的中點.
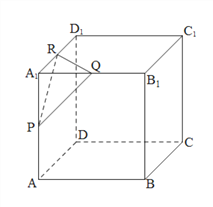
(Ⅰ)求二面角![]() 的余弦值;
的余弦值;
(Ⅱ)以![]() 為底面作正三棱柱,若此三棱柱另一底面三個頂點也都在該正方體的表面上,求這個正三棱柱的高.
為底面作正三棱柱,若此三棱柱另一底面三個頂點也都在該正方體的表面上,求這個正三棱柱的高.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某食品企業一個月內被消費者投訴的次數用![]() 表示.據統計,隨機變量
表示.據統計,隨機變量![]() 的概率分布如下表所示.
的概率分布如下表所示.
| 0 | 1 | 2 | 3 |
| 0.1 | 0.3 |
|
|
(1)求![]() 的值和
的值和![]() 的數學期望;
的數學期望;
(2)假設一月份與二月份被消費者投訴的次數互不影響,求該企業在這兩個月內共被消費者投訴2次的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠計劃出售一種產品,經銷人員并不是根據生產成本來確定這種產品的價格,而是通過對經營產品的零售商對于不同的價格情況下他們會進多少貨進行調查,通過調查確定了關系式P=-750x+15000,其中P為零售商進貨的數量(單位:件),x為零售商支付的每件產品價格(單位:元).現估計生產這種產品每件的材料和勞動生產費用為4元,并且工廠生產這種產品的總固定成本為7000元(固定成本是除材料和勞動費用以外的其他費用),為獲得最大利潤,工廠應對零售商每件收取多少元?并求此時的最大利潤.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 為奇函數,且x=-1處取得極大 值2.
為奇函數,且x=-1處取得極大 值2.
(1)求f(x)的解析式;
(2)過點A(1,t) ![]() 可作函數f(x)圖像的三條切線,求實數t的取值范圍;
可作函數f(x)圖像的三條切線,求實數t的取值范圍;
(3)若![]() 對于任意的
對于任意的![]() 恒成立,求實數m取值范圍.
恒成立,求實數m取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,三棱柱中ABC﹣A1B1C1中,點A1在平面ABC內的射影D為棱AC的中點,側面A1ACC1為邊長為2的菱形,AC⊥CB,BC=1. 
(1)證明:AC1⊥平面A1BC;
(2)求二面角B﹣A1C﹣B1的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ex﹣ ![]() ,g(x)=2ln(x+1)+e﹣x .
,g(x)=2ln(x+1)+e﹣x .
(1)x∈(﹣1,+∞)時,證明:f(x)>0;
(2)a>0,若g(x)≤ax+1,求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C: ![]() 的長軸長為4,焦距為
的長軸長為4,焦距為![]() .
.
(Ⅰ)求橢圓C的方程;

(Ⅱ)過動點M(0,m)(m>0)的直線交x軸與點N,交C于點A,P(P在第一象限),且M是線段PN的中點,過點P作x軸的垂線交C于另一點Q,延長線QM交C于點B.
(i)設直線PM、QM的斜率分別為k、![]() ,證明
,證明![]() 為定值.
為定值.
(ii)求直線AB的斜率的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com