
【題目】如圖,已知過點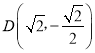 的橢圓
的橢圓![]() 的離心率為
的離心率為![]() ,左頂點和上頂點分別為A,B.
,左頂點和上頂點分別為A,B.
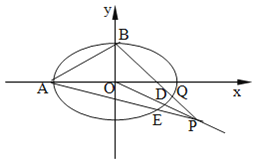
(1)求橢圓的標準方程;
(2)若P為線段OD延長線上一點,直線PA交橢圓于另一點E,直線PB交橢圓于另一點Q.
①求直線PA與PB的斜率之積;
②判斷直線AB與EQ是否平行?并說明理由.
【答案】(1)![]() 1.(2) ①
1.(2) ① ![]() .②平行.理由見解析
.②平行.理由見解析
【解析】
(1)離心率值轉化為![]() 關系,再把點
關系,再把點![]() 坐標代入方程,即可求出橢圓標準方程;
坐標代入方程,即可求出橢圓標準方程;
(2)①求出![]() 方程,設出
方程,設出![]() 點坐標,可求出直線PA與PB的斜率之積;
點坐標,可求出直線PA與PB的斜率之積;
②求出直線![]() 方程,分別與橢圓方程聯立,求出
方程,分別與橢圓方程聯立,求出![]() 兩點坐標,代入斜率公式,求出直線
兩點坐標,代入斜率公式,求出直線![]() 的斜率,然后再判斷與直線
的斜率,然后再判斷與直線![]() 是否平行.
是否平行.
(1)∵橢圓過點D(![]() ,
,![]() ),且離心率為
),且離心率為![]()
![]()
∴![]() ,
,
∴橢圓的方程為![]() 1.
1.
(2)①由(1)知A(﹣2,0),B(0,1),
直線OD方程為y![]() ,
,
點P在直線OD上,設P(﹣2y0,y0),
kPAkPB![]() .
.
②設E(x1,y1),Q(x2,y2),
聯立直線AP:y![]() 與橢圓的方程得,
與橢圓的方程得,
(2y02﹣2y0+1)x2+4y02x+8y0﹣4=0,
∴﹣2+x1![]() ,
,
∴x1![]() ,y1
,y1![]() ,
,
聯立直線BP:y![]() 與橢圓的方程得,
與橢圓的方程得,
![]() ,
,
∴x2![]() ,y2
,y2![]() ,
,
∴![]()
又因為kAB![]() ,∴kAB=kEQ,
,∴kAB=kEQ,
∴直線AB與EQ是平行.


 三新快車金牌周周練系列答案
三新快車金牌周周練系列答案科目:高中數學 來源: 題型:
【題目】某興趣小組在科學館的帕斯卡三角儀器前進行探究實驗.如圖所示,每次使一個實心小球從帕斯卡三角儀器的頂部入口落下,當它在依次碰到每層的菱形擋板時,會等可能地向左或者向右落下,在最底層的7個出口處各放置一個容器接住小球,該小組連續進行200次試驗,并統計容器中的小球個數得到柱狀圖:
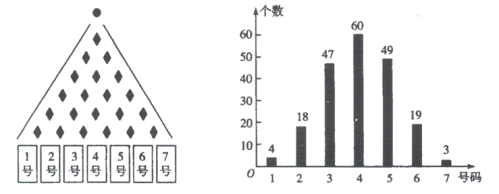
(Ⅰ)用該實驗來估測小球落入4號容器的概率,若估測結果的誤差小于![]() ,則稱該實驗是成功的.試問:該興趣小組進行的實驗是否成功?(誤差
,則稱該實驗是成功的.試問:該興趣小組進行的實驗是否成功?(誤差![]() )
)
(Ⅱ)再取3個小球進行試驗,設其中落入4號容器的小球個數為![]() ,求
,求![]() 的分布列與數學期望.(計算時采用概率的理論值)
的分布列與數學期望.(計算時采用概率的理論值)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國是世界上嚴重缺水的國家,城市缺水問題較為突出.某市政府為了節約用水,市民用水擬實行階梯水價.每人月用水量中不超過![]() 立方米的部分按4元/立方米收費,超出
立方米的部分按4元/立方米收費,超出![]() 立方米的部分按10元/立方米收費.從該市隨機調查了10 000位居民,獲得了他們某月的用水量數據,整理得到如下頻率分布直方圖:
立方米的部分按10元/立方米收費.從該市隨機調查了10 000位居民,獲得了他們某月的用水量數據,整理得到如下頻率分布直方圖:

(1)如果![]() 為整數,那么根據此次調查,為使80%以上居民在該月的用水價格為4元/立方米,
為整數,那么根據此次調查,為使80%以上居民在該月的用水價格為4元/立方米,![]() 至少定為多少?
至少定為多少?
(2)假設同組中的每個數據用該組區間的右端點值代替.當![]() =3時,試完成該10000位居民該月水費的頻率分布表,并估計該市居民該月的人均水費.
=3時,試完成該10000位居民該月水費的頻率分布表,并估計該市居民該月的人均水費.
組號 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
分組 |
|
|
|
|
|
|
|
|
頻率 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知雙曲線![]() 的右頂點為A,拋物線的焦點與點A重合.
的右頂點為A,拋物線的焦點與點A重合.
(1)求拋物線的標準方程;
(2)若直線l過點A且斜率為雙曲線的離心率,求直線l被拋物線截得的弦長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,GH是東西方向的公路北側的邊緣線,某公司準備在GH上的一點B的正北方向的A處建設一倉庫,設![]() ,并在公路北側建造邊長為
,并在公路北側建造邊長為![]() 的正方形無頂中轉站CDEF(其中EF在GH上),現從倉庫A向GH和中轉站分別修兩條道路AB,AC,已知AB=AC+1,且
的正方形無頂中轉站CDEF(其中EF在GH上),現從倉庫A向GH和中轉站分別修兩條道路AB,AC,已知AB=AC+1,且![]() .
.
(1)求![]() 關于
關于![]() 的函數解析式,并求出定義域;
的函數解析式,并求出定義域;
(2)如果中轉站四堵圍墻造價為10萬元/km,兩條道路造價為30萬元/km,問:![]() 取何值時,該公司建設中轉站圍墻和兩條道路總造價M最低.
取何值時,該公司建設中轉站圍墻和兩條道路總造價M最低.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某老師是省級課題組的成員,主要研究課堂教學目標達成度,為方便研究,從實驗班中隨機抽取30次的隨堂測試成績進行數據分析![]() 已知學生甲的30次隨堂測試成績如下
已知學生甲的30次隨堂測試成績如下![]() 滿分為100分
滿分為100分![]() :
:

![]() 把學生甲的成績按
把學生甲的成績按![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分成6組,列出頻率分布表,并畫出頻率分布直方圖;
分成6組,列出頻率分布表,并畫出頻率分布直方圖;
![]() 規定隨堂測試成績80分以上
規定隨堂測試成績80分以上![]() 含80分
含80分![]() 為優秀,為幫助學生甲提高成績,選取學生乙,對甲與乙的隨堂測試成績進行對比分析,甲與乙測試成績是否為優秀相互獨立
為優秀,為幫助學生甲提高成績,選取學生乙,對甲與乙的隨堂測試成績進行對比分析,甲與乙測試成績是否為優秀相互獨立![]() 已知甲成績優秀的概率為
已知甲成績優秀的概率為![]() 以頻率估計概率
以頻率估計概率![]() ,乙成績優秀的概率為
,乙成績優秀的概率為![]() ,若
,若![]() ,則此二人適合為學習上互幫互助的“對子”
,則此二人適合為學習上互幫互助的“對子”![]() 在一次隨堂測試中,記
在一次隨堂測試中,記![]() 為兩人中獲得優秀的人數,已知
為兩人中獲得優秀的人數,已知![]() ,問二人是否適合結為“對子”?
,問二人是否適合結為“對子”?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某化工企業2018年年底投入100萬元,購入一套污水處理設備。該設備每年的運轉費用是0.5萬元,此外,每年都要花費一定的維護費,第一年的維護費為2萬元,由于設備老化,以后每年的維護費都比上一年增加2萬元。設該企業使用該設備![]() 年的年平均污水處理費用為
年的年平均污水處理費用為![]() (單位:萬元)
(單位:萬元)
(1)用![]() 表示
表示![]() ;
;
(2)當該企業的年平均污水處理費用最低時,企業需重新更換新的污水處理設備。則該企業幾年后需要重新更換新的污水處理設備。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() :
:![]() ,過坐標原點
,過坐標原點![]() 的直線
的直線![]() 交
交![]() 于
于![]() ,
,![]() 兩點,點
兩點,點![]() 在第一象限,
在第一象限,![]() 軸,垂足為
軸,垂足為![]() .連結
.連結![]() 并延長交
并延長交![]() 于點
于點![]() .
.
(1)設![]() 到直線
到直線![]() 的距離為
的距離為![]() ,求
,求![]() 的取值范圍;
的取值范圍;
(2)求![]() 面積的最大值及此時直線
面積的最大值及此時直線![]() 的方程.
的方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com