
【題目】設不等式![]() 確定的平面區域為U,
確定的平面區域為U,![]() 確定的平面區域為V.
確定的平面區域為V.
(1)定義橫、縱坐標為整數的點為“整點”,在區域U內任取3個整點,求這些整點中恰有2個整點在區域V內的概率;
(2)設集合![]() ;集合
;集合![]() 若從集合A到集合B可以建立m個不同的映射?從集合B到集合A可以建立n個不同的映射,求m,n的值.
若從集合A到集合B可以建立m個不同的映射?從集合B到集合A可以建立n個不同的映射,求m,n的值.
 應用題天天練四川大學出版社系列答案
應用題天天練四川大學出版社系列答案科目:高中數學 來源: 題型:
【題目】為了調查甲、乙兩個網站受歡迎的程度,隨機選取了14天,統計上午8:00~10:00各自的點擊量,得到如圖所示的莖葉圖,根據莖葉圖回答下列問題.

(1)甲、乙兩個網站點擊量的極差分別是多少?
(2)甲網站點擊量在[10,40]間的頻率是多少?
(3)甲、乙兩網站哪個更受歡迎?并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系中,已知橢圓![]() 經過點
經過點![]() ,且其左右焦點的坐標分別是
,且其左右焦點的坐標分別是![]() ,
,![]() .
.
(1)求橢圓![]() 的離心率及標準方程;
的離心率及標準方程;
(2)設![]() 為動點,其中
為動點,其中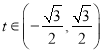 ,直線
,直線![]() 經過點
經過點![]() 且與橢圓
且與橢圓![]() 相交于
相交于![]() ,
,![]() 兩點,若
兩點,若![]() 為
為![]() 的中點,是否存在定點
的中點,是否存在定點![]() ,使
,使![]() 恒成立?若存在,求點
恒成立?若存在,求點![]() 的坐標;若不存在,說明理由
的坐標;若不存在,說明理由
查看答案和解析>>
科目:高中數學 來源: 題型:
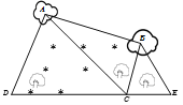
【題目】如圖,為了測量某濕地![]() 兩點間的距離,觀察者找到在同一直線上的三點
兩點間的距離,觀察者找到在同一直線上的三點![]() .從
.從![]() 點測得
點測得![]() ,從
,從![]() 點測得
點測得![]() ,
,![]() ,從
,從![]() 點測得
點測得![]() .若測得
.若測得![]() ,
,![]() (單位:百米),則
(單位:百米),則![]() 兩點的距離為( )
兩點的距離為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在四棱錐P-ABCD中,ABCD為梯形,AB//CD,BC⊥AB,AB=2![]() ,BC=
,BC=![]() ,CD=PC=
,CD=PC=![]() 。
。
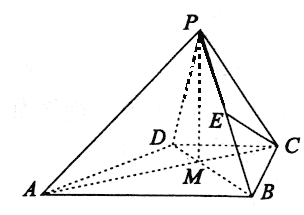
(I)點E在線段PB上,滿足CE//平面PAD,求![]() 的值。
的值。
(II)已知AC與BD的交點為M,若PM=1,且平面PAC⊥平面ABCD,求二面角P-BC-M平面角的余弦值。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面真角坐標系xOy中,曲線![]() 的參數方程為
的參數方程為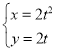 (t為參數),以原點O為極點,x軸正半軸為極軸,建立根坐標系.曲線
(t為參數),以原點O為極點,x軸正半軸為極軸,建立根坐標系.曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求曲線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)若曲線![]() 與曲線
與曲線![]() 交于M,N兩點,直線OM和ON的斜率分別為
交于M,N兩點,直線OM和ON的斜率分別為![]() 和
和![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,已知曲線C由圓弧C1和圓弧C2相接而成,兩相接點M,N均在直線x=5上.圓弧C1的圓心是坐標原點O,半徑為13;圓弧C2過點A(29,0).
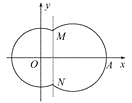
(1)求圓弧C2的方程.
(2)曲線C上是否存在點P,滿足PA=![]() PO?若存在,指出有幾個這樣的點;若不存在,請說明理由.
PO?若存在,指出有幾個這樣的點;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左,右焦點分別為F1, F2,直線l1過點F1且垂直于橢圓的長軸,動直線l2垂直l1于點P,線段PF2的垂直平分線交l2于點M.
的左,右焦點分別為F1, F2,直線l1過點F1且垂直于橢圓的長軸,動直線l2垂直l1于點P,線段PF2的垂直平分線交l2于點M.
(1)求點M的軌跡![]() 的方程;
的方程;
(2)設![]() 與x軸交于點Q,
與x軸交于點Q, ![]() 上不同于點Q的兩點R、S,且滿足
上不同于點Q的兩點R、S,且滿足![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(1)若![]() ,
,![]() 且
且![]() ,則
,則![]() 的取值范圍是______.
的取值范圍是______.
(2)若![]() ,
,![]() ,且
,且![]() ,則
,則![]() 的取值范圍是______.
的取值范圍是______.
(3)已知![]() ,且
,且![]() ,則
,則![]() 的最小值是______.
的最小值是______.
(4)已知實數![]() ,
,![]() ,若
,若![]() ,
,![]() ,且
,且![]() ,則
,則![]() 的最小值______.
的最小值______.
(5)已知實數![]() ,
,![]() ,若
,若![]() ,
,![]() ,則
,則![]() 的最小值______.
的最小值______.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com