【題目】對于給定的正整數k,若數列{an}滿足
=2kan對任意正整數n(n> k) 總成立，則稱數列{an} 是“P(k)數列”.
(1)證明：等差數列{an}是“P(3)數列”；
若數列{an}既是“P(2)數列”，又是“P(3)數列”，證明：{an}是等差數列.
【答案】（1）見解析（2）見解析
【解析】試題分析：（1）利用等差數列性質得
，即得
，再根據定義即可判斷；（2）先根據定義得
， 
，再將條件集中消元： 
， 
，即得
，最后驗證起始項也滿足即可．
試題解析：證明:（1）因為
是等差數列，設其公差為
，則
，
從而，當
時， 
， 
所以
，
因此等差數列
是“
數列”.
（2）數列
既是“
數列”，又是“
數列”，因此，
當
時， 
，①
當
時， 
.②
由①知， 
，③
，④
將③④代入②，得
，其中
，
所以
是等差數列，設其公差為
.
在①中，取
，則
，所以
，
在①中，取
，則
，所以
，
所以數列
是等差數列.
點睛:證明
為等差數列的方法：①用定義證明： 
為常數）；②用等差中項證明： 
；③通項法： 
為關于
的一次函數；④前
項和法： 
．
科目：高中數學 來源： 題型：
【題目】張老師給學生出了一道題，“試寫一個程序框圖，計算S=1+ 
+ 
+ 
+ 
”．發現同學們有如下幾種做法，其中有一個是錯誤的，這個錯誤的做法是（ ）
A.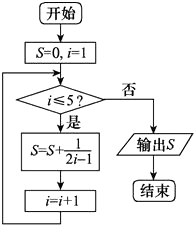
B.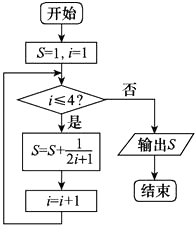
C.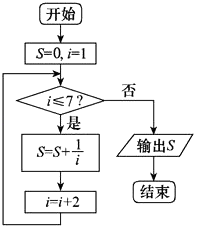
D.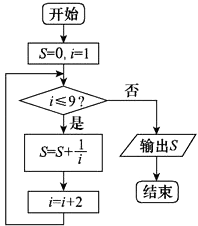
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知正數數列{an}的前n項和為Sn ， 點P（an ， Sn）在函數f（x）= 
x2+ x上，已知b1=1，3bn﹣2bn﹣1=0（n≥2，n∈N*），
（1）求數列{an}的通項公式；
（2）若cn=anbn ， 求數列{cn}的前n項和Tn；
（3）是否存在整數m，M，使得m＜Tn＜M對任意正整數n恒成立，且M﹣m=9，說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知長方體AC1中，AD=AB=2，AA1=1，E為D1C1的中點，如圖所示．
（Ⅰ）在所給圖中畫出平面ABD1與平面B1EC的交線（不必說明理由）；
（Ⅱ）證明：BD1∥平面B1EC；
（Ⅲ）求平面ABD1與平面B1EC所成銳二面角的大小．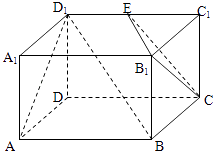
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，三棱柱ABC﹣A1B1C1中，側棱垂直底面，∠ACB=90°，AC=BC= 
AA1 ， D是棱AA1的中點．
（Ⅰ）證明：平面BDC1⊥平面BDC
（Ⅱ）平面BDC1分此棱柱為兩部分，求這兩部分體積的比．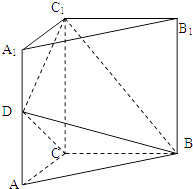
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】函數f（x）=|2x﹣1|，定義f1（x）=x，fn+1（x）=f（fn（x）），已知函數g（x）=fm（x）﹣x有8個零點，則m的值為（ ）
A.8
B.4
C.3
D.2
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知數列{an}滿足：a1=1，an+1= 
an+ 
（n∈N*）．
（1）求最小的正實數M，使得對任意的n∈N* ， 恒有0＜an≤M．
（2）求證：對任意的n∈N* ， 恒有 
≤an≤ 
．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知： 
=（2sinx，2cosx）， 
=（cosx，﹣cosx），f（x）= 
．
（1）若 與 共線，且x∈（ 
，π），求x的值；
（2）求函數f（x）的周期；
（3）若對任意x∈[0， ]不等式m﹣2≤f（x）≤m+ 
恒成立，求實數m的取值范圍．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
