
【題目】隨著智能手機的普及,使用手機上網成為了人們日常生活的一部分,很多消費者對手機流量的需求越來越大.長沙某通信公司為了更好地滿足消費者對流量的需求,準備推出一款流量包.該通信公司選了5個城市(總人數、經濟發展情況、消費能力等方面比較接近)采用不同的定價方案作為試點,經過一個月的統計,發現該流量包的定價![]() :(單位:元/月)和購買人數
:(單位:元/月)和購買人數![]() (單位:萬人)的關系如表:
(單位:萬人)的關系如表:
![]()
(1)根據表中的數據,運用相關系數進行分析說明,是否可以用線性回歸模型擬合![]() 與
與![]() 的關系?并指出是正相關還是負相關;
的關系?并指出是正相關還是負相關;
(2)①求出![]() 關于
關于![]() 的回歸方程;
的回歸方程;
②若該通信公司在一個類似于試點的城市中將這款流量包的價格定位25元/ 月,請用所求回歸方程預測長沙市一個月內購買該流量包的人數能否超過20 萬人.
參考數據:![]() ,
,![]() ,
,![]() .
.
參考公式:相關系數 ,回歸直線方程
,回歸直線方程![]() ,
,
其中 ,
,![]() .
.
科目:高中數學 來源: 題型:
【題目】某公司計劃購買1臺機器,該種機器使用三年后即被淘汰.在購進機器時,可以一次性額外購買幾次維修服務,每次維修服務費用200元,另外實際維修一次還需向維修人員支付小費,小費每次50元.在機器使用期間,如果維修次數超過購機時購買的維修服務次數,則每維修一次需支付維修服務費用500元,無需支付小費.現需決策在購買機器時應同時一次性購買幾次維修服務,為此搜集并整理了100臺這種機器在三年使用期內的維修次數,得下面統計表:
維修次數 | 8 | 9 | 10 | 11 | 12 |
頻數 | 10 | 20 | 30 | 30 | 10 |
記x表示1臺機器在三年使用期內的維修次數,y表示1臺機器在維修上所需的費用(單位:元),![]() 表示購機的同時購買的維修服務次數.
表示購機的同時購買的維修服務次數.
(1)若![]() =10,求y與x的函數解析式;
=10,求y與x的函數解析式;
(2)若要求“維修次數不大于![]() ”的頻率不小于0.8,求n的最小值;
”的頻率不小于0.8,求n的最小值;
(3)假設這100臺機器在購機的同時每臺都購買10次維修服務,或每臺都購買11次維修服務,分別計算這100臺機器在維修上所需費用的平均數,以此作為決策依據,購買1臺機器的同時應購買10次還是11次維修服務?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如果函數![]() 的定義域為
的定義域為![]() ,且存在實常數
,且存在實常數![]() ,使得對于定義域內任意
,使得對于定義域內任意![]() ,都有
,都有![]() 成立,則稱此函數
成立,則稱此函數![]() 具有“性質
具有“性質![]() ”.
”.
(1)判斷函數![]() 是否具有“
是否具有“![]() 性質”,若具有“
性質”,若具有“![]() 性質”,求出所有
性質”,求出所有![]() 的值的集合,若不具有“
的值的集合,若不具有“![]() 性質”,請說明理由;
性質”,請說明理由;
(2)已知函數![]() 具有“
具有“![]() 性質”,且當
性質”,且當![]() 時,
時,![]() ,求函數
,求函數![]() 在區間
在區間![]() 上的值域;
上的值域;
(3)已知函數![]() 既具有“
既具有“![]() 性質”,又具有“
性質”,又具有“![]() 性質”,且當
性質”,且當![]() 時,
時,![]() ,若函數
,若函數![]() 的圖像與直線
的圖像與直線![]() 有2017個公共點,求實數
有2017個公共點,求實數![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】繼共享單車之后,又一種新型的出行方式------“共享汽車”也開始亮相北上廣深等十余大中城市,一款叫“一度用車”的共享汽車在廣州提供的車型是“奇瑞eQ”,每次租車收費按行駛里程加用車時間,標準是“1元/公里+0.1元/分鐘”,李先生家離上班地點10公里,每天租用共享汽車上下班,由于堵車因素,每次路上開車花費的時間是一個隨機變量,根據一段時間統計40次路上開車花費時間在各時間段內的情況如下:
時間(分鐘) |
|
|
|
|
|
次數 | 8 | 14 | 8 | 8 | 2 |
以各時間段發生的頻率視為概率,假設每次路上開車花費的時間視為用車時間,范圍為![]() 分鐘.
分鐘.
(Ⅰ)若李先生上.下班時租用一次共享汽車路上開車不超過45分鐘,便是所有可選擇的交通工具中的一次最優選擇,設![]() 是4次使用共享汽車中最優選擇的次數,求
是4次使用共享汽車中最優選擇的次數,求![]() 的分布列和期望.
的分布列和期望.
(Ⅱ)若李先生每天上下班使用共享汽車2次,一個月(以20天計算)平均用車費用大約是多少(同一時段,用該區間的中點值作代表).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,橢圓短軸的一個端點與兩個焦點構成的三角形的面積為
,橢圓短軸的一個端點與兩個焦點構成的三角形的面積為![]() .
.
(1)求橢圓![]() 的方程式;
的方程式;
(2)已知動直線![]() 與橢圓
與橢圓![]() 相交于
相交于![]() 兩點.
兩點.
①若線段![]() 中點的橫坐標為
中點的橫坐標為![]() ,求斜率
,求斜率![]() 的值;
的值;
②已知點![]() ,求證:
,求證: ![]() 為定值.
為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
以平面直角坐標系![]() 的原點為極點,
的原點為極點,![]() 軸的正半軸為極軸,建立極坐標系,且兩種坐標系中采取相同的單位長度.曲線
軸的正半軸為極軸,建立極坐標系,且兩種坐標系中采取相同的單位長度.曲線![]() 的極坐標方程是
的極坐標方程是![]() ,直線的參數方程是
,直線的參數方程是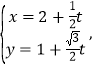 (
(![]() 為參數).
為參數).
(1)求曲線![]() 的直角坐標方程與直線
的直角坐標方程與直線![]() 的普通方程;
的普通方程;
(2)設點![]() ,若直線
,若直線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點,求
兩點,求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com