
【題目】設![]() ,
,![]() 是拋物線
是拋物線![]() 上的兩個不同的點,
上的兩個不同的點,![]() 是坐標原點.若直線
是坐標原點.若直線![]() 與
與![]() 的斜率之積為
的斜率之積為![]() ,則( ).
,則( ).
A.![]() B.以
B.以![]() 為直徑的圓的面積大于
為直徑的圓的面積大于![]()
C.直線![]() 過定點
過定點![]() D.點
D.點![]() 到直線
到直線![]() 的距離不大于2
的距離不大于2
【答案】CD
【解析】
通過![]() 軸時的特殊情況,判斷A、B選項不正確;當直線
軸時的特殊情況,判斷A、B選項不正確;當直線![]() 與
與![]() 軸不垂直時,設
軸不垂直時,設![]() 直線方程,通過推理論證,得出直線過定點
直線方程,通過推理論證,得出直線過定點![]() ,進而得出點
,進而得出點![]() 到直線
到直線![]() 的距離最大值即為O、Q兩點間的距離,進而得出CD正確.
的距離最大值即為O、Q兩點間的距離,進而得出CD正確.
不妨設![]() 為第一象限內的點,
為第一象限內的點,
①當直線![]() 軸時,
軸時,![]() ,由
,由![]() ,
,
得![]() ,
,![]() ,
,
所以直線![]() ,
,![]() 的方程分別為:
的方程分別為:![]() 和
和![]() .
.
與拋物線方程聯立,得![]() ,
,![]() ,
,
所以直線![]() 的方程為
的方程為![]() ,此時
,此時![]() ,
,
以![]() 為直徑的圓的面積
為直徑的圓的面積![]() ,故A、B不正確.
,故A、B不正確.
②當直線![]() 與
與![]() 軸不垂直時,設直線
軸不垂直時,設直線![]() 的方程為
的方程為![]() ,
,
與拋物線方程聯立消去![]() ,得
,得![]() ,則
,則![]() .
.
設![]() ,
,![]() ,則
,則![]() .
.
因為![]() ,所以
,所以![]() ,
,
則![]() ,則
,則![]() ,
,
所以![]() ,即
,即![]() ,
,
所以直線![]() 的方程為
的方程為![]() ,即
,即![]() .
.
綜上可知,直線![]() 為恒過定點
為恒過定點![]() 的動直線,故C正確;
的動直線,故C正確;
易知當![]() 時,原點
時,原點![]() 到直線
到直線![]() 的距離最大,最大距離為2,
的距離最大,最大距離為2,
即原點![]() 到直線
到直線![]() 的距離不大于2.故D正確.
的距離不大于2.故D正確.
故選:CD


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
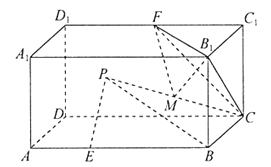
【題目】古希臘數學家阿波羅尼奧斯發現:平面上到兩定點![]() ,
,![]() 距離之比為常數
距離之比為常數![]() 且
且![]() 的點的軌跡是一個圓心在直線
的點的軌跡是一個圓心在直線![]() 上的圓,該圓簡稱為阿氏圓.根據以上信息,解決下面的問題:如圖,在長方體
上的圓,該圓簡稱為阿氏圓.根據以上信息,解決下面的問題:如圖,在長方體![]() 中,
中,![]() ,點
,點![]() 在棱
在棱![]() 上,
上,![]() ,動點
,動點![]() 滿足
滿足![]() .若點
.若點![]() 在平面
在平面![]() 內運動,則點
內運動,則點![]() 所形成的阿氏圓的半徑為________;若點
所形成的阿氏圓的半徑為________;若點![]() 在長方體
在長方體![]() 內部運動,
內部運動,![]() 為棱
為棱![]() 的中點,
的中點,![]() 為
為![]() 的中點,則三棱錐
的中點,則三棱錐![]() 的體積的最小值為___________.
的體積的最小值為___________.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,已知焦點為![]() 的拋物線
的拋物線![]() 上有一動點
上有一動點![]() ,過點
,過點![]() 作拋物線的切線
作拋物線的切線![]() 交
交![]() 軸于點
軸于點![]() .
.
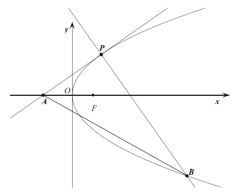
(1)判斷線段![]() 的中垂線是否過定點,若是求出定點坐標,若不是說明理由;
的中垂線是否過定點,若是求出定點坐標,若不是說明理由;
(2)過點![]() 作
作![]() 的垂線交拋物線于另一點
的垂線交拋物線于另一點![]() ,求
,求![]() 面積的最小值.
面積的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在矩形![]() 中,
中,![]() 為邊
為邊![]() 的中點,將
的中點,將![]() 沿直線
沿直線![]() 翻轉成
翻轉成![]() (
(![]() 平面
平面![]() ).若
).若![]() 分別為線段
分別為線段![]() 的中點,則在
的中點,則在![]() 翻轉過程中,下列說法正確的是( )
翻轉過程中,下列說法正確的是( )
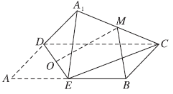
A.與平面![]() 垂直的直線必與直線
垂直的直線必與直線![]() 垂直
垂直
B.異面直線![]() 與
與![]() 所成的角是定值
所成的角是定值
C.一定存在某個位置,使![]()
D.三棱錐![]() 外接球半徑與棱
外接球半徑與棱![]() 的長之比為定值
的長之比為定值
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】臺球運動已有五、六百年的歷史,參與者用球桿在臺上擊球.若和光線一樣,臺球在球臺上碰到障礙物后也遵從反射定律如圖,有一張長方形球臺ABCD,![]() ,現從角落A沿角
,現從角落A沿角![]() 的方向把球打出去,球經2次碰撞球臺內沿后進入角落C的球袋中,則
的方向把球打出去,球經2次碰撞球臺內沿后進入角落C的球袋中,則![]() 的值為( )
的值為( )
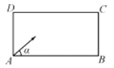
A.![]() B.
B.![]() C.1D.
C.1D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】農歷五月初五是端午節,民間有吃粽子的習慣,粽子又稱粽粒,古稱角黍,是端午節大家都會品嘗的食品.如圖,平行四邊形形狀的紙片是由六個邊長為2的正三角形構成的,將它沿虛線折起來,可以得到如圖所示粽子形狀的六面體,則該六面體的體積為_________;若該六面體內有一球,當該球體積最大時,球的表面積是__________.
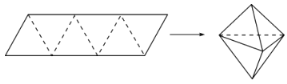
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知矩形![]() 和菱形
和菱形![]() 所在平面互相垂直,如圖,其中
所在平面互相垂直,如圖,其中![]() ,
, ![]() ,
, ![]() ,點
,點![]() 為線段
為線段![]() 的中點.
的中點.
(Ⅰ)試問在線段![]() 上是否存在點
上是否存在點![]() ,使得直線
,使得直線![]() 平面
平面![]() ?若存在,請證明
?若存在,請證明![]() 平面
平面![]() ,并求出
,并求出![]() 的值,若不存在,請說明理由;
的值,若不存在,請說明理由;
(Ⅱ)求二面角![]() 的正弦值.
的正弦值.
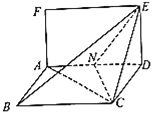
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com