
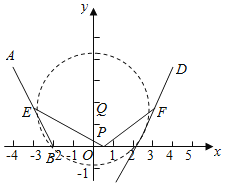
【題目】如圖,在折線![]() 中,
中,![]() ,
,![]() ,
,![]() 分別是
分別是![]() 的中點,若折線上滿足條件
的中點,若折線上滿足條件![]() 的點
的點![]() 至少有
至少有![]() 個,則實數
個,則實數![]() 的取值范圍是___________.
的取值范圍是___________.

【答案】![]()
【解析】
以BC的垂直平分線為y軸,以BC為x軸,建立如圖所示的平面直角坐標系,分別表示各個點的坐標,設P(x,y),根據向量的數量積可得當k+9>0時,點P的軌跡為以(0,![]() )為圓心,以
)為圓心,以![]() 為半徑的圓,結合圖象,即可求出滿足條件
為半徑的圓,結合圖象,即可求出滿足條件![]() 的點P至少有4個的k的取值范圍.
的點P至少有4個的k的取值范圍.
解:以BC的垂直平分線為y軸,以BC為x軸,建立如圖所示的平面直角坐標系,
∵AB=BC=CD=4,∠ABC=∠BCD=120°,
∴B(﹣2.0),C(2,0),A(﹣4,2![]() ),D(4,2
),D(4,2![]() ),
),
∵E、F分別是AB、CD的中點,
∴E(﹣3,![]() ),F(3,
),F(3,![]() ),
),
設P(x,y),﹣4≤x≤4,0≤y≤2![]() ,
,
∵![]() ,
,
∴(﹣3﹣x,![]() (3﹣x,
(3﹣x,![]() y)=
y)=![]() ,
,
即![]() ,
,
當k+9>0時,點P的軌跡為以(0,![]() )為圓心,以
)為圓心,以![]() 為半徑的圓,
為半徑的圓,
當圓與直線DC相切時,此時圓的半徑r![]() ,此時點有2個,
,此時點有2個,
當圓經過點C時,此時圓的半徑為r![]() ,此時點P有4個,
,此時點P有4個,
∵滿足條件![]() 的點P至少有4個,結合圖象可得,
的點P至少有4個,結合圖象可得,
∴![]() k+9≤7,
k+9≤7,
解得![]() k≤﹣2,
k≤﹣2,
故實數k的取值范圍為[![]() ,﹣2],
,﹣2],
故答案為:[![]() ,﹣2]
,﹣2]


科目:高中數學 來源: 題型:
【題目】春節來臨之際,某超市為了確定此次春節年貨的進貨方案,統計去年春節前后50天年貨的日銷售量(單位:kg),得到如圖所示的頻率分布直方圖.
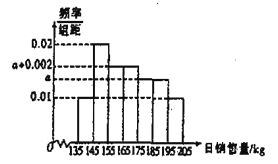
(1)求這50天超市日銷售量![]() 的平均數;(視頻率為概率,以各組區間的中點值代表該組的值)
的平均數;(視頻率為概率,以各組區間的中點值代表該組的值)
(2)先從日銷售在![]() ,
,![]() ,
,![]() 內的天數中,按分層抽樣隨機抽取4天進行比較研究,再從中選2天,求這2天的日銷售量都在
內的天數中,按分層抽樣隨機抽取4天進行比較研究,再從中選2天,求這2天的日銷售量都在![]() 內的概率.
內的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(Ⅰ)若關于![]() 的不等式
的不等式![]() 在
在![]() 上恒成立,求
上恒成立,求![]() 的取值范圍;
的取值范圍;
(Ⅱ)設函數![]() ,在(Ⅰ)的條件下,試判斷
,在(Ⅰ)的條件下,試判斷![]() 在
在![]() 上是否存在極值.若存在,判斷極值的正負;若不存在,請說明理由.
上是否存在極值.若存在,判斷極值的正負;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() 滿足
滿足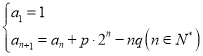 ,其中
,其中![]() .
.
(1)若數列前四項![]() ,
,![]() ,
,![]() ,
,![]() 依次成等差數列,求
依次成等差數列,求![]() ,
,![]() 的值;
的值;
(2)若![]() ,且數列
,且數列![]() 為等比數列,求
為等比數列,求![]() 的值;
的值;
(3)若![]() ,且
,且![]() 是數列
是數列![]() 的最小項,求
的最小項,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】垃圾分一分,城市美十分;垃圾分類,人人有責.某市為進一步推進生活垃圾分類工作,調動全民參與的積極性,舉辦了“垃圾分類游戲挑戰賽”.據統計,在為期![]() 個月的活動中,共有
個月的活動中,共有![]() 萬人次參與.為鼓勵市民積極參與活動,市文明辦隨機抽取
萬人次參與.為鼓勵市民積極參與活動,市文明辦隨機抽取![]() 名參與該活動的網友,以他們單次游戲得分作為樣本進行分析,由此得到如下頻數分布表:
名參與該活動的網友,以他們單次游戲得分作為樣本進行分析,由此得到如下頻數分布表:
單次游戲得分 |
|
|
|
|
|
|
頻數 |
|
|
|
|
|
|
(1)根據數據,估計參與活動的網友單次游戲得分的平均值及標準差(同一組中的數據用該組區間的中點值作代表);(其中標準差的計算結果要求精確到![]() )
)
(2)若要從單次游戲得分在![]() 、
、![]() 、
、![]() 的三組參與者中,用分層抽樣的方法選取
的三組參與者中,用分層抽樣的方法選取![]() 人進行電話回訪,再從這
人進行電話回訪,再從這![]() 人中任選
人中任選![]() 人贈送話費,求此
人贈送話費,求此![]() 人單次游戲得分不在同一組內的概率.
人單次游戲得分不在同一組內的概率.
附:![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】華東師大二附中樂東黃流中學位于我國南海邊,有一片美麗的沙灘和一彎天然的海濱浴場.如圖,海岸線MAN,![]() ,
,![]() (海岸線MAN上方是大海),現用長為BC的欄網圍成一個三角形學生游泳場所,其中
(海岸線MAN上方是大海),現用長為BC的欄網圍成一個三角形學生游泳場所,其中![]() .
.
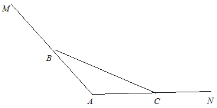
(1)若![]() ,求三角形游泳場所面積最大值;
,求三角形游泳場所面積最大值;
(2)若BC=600,![]() ,由于學生人數的增加需要擴大游泳場所面積,現在折線MBCN上方選點D,現用長為BD,DC的欄圍成一個四邊形游泳場所DBAC,使
,由于學生人數的增加需要擴大游泳場所面積,現在折線MBCN上方選點D,現用長為BD,DC的欄圍成一個四邊形游泳場所DBAC,使![]() ,求四邊形游泳場所DBAC的最大面積.
,求四邊形游泳場所DBAC的最大面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設F1、F2分別為橢圓C:![]() =1(a>b>0)的左、右焦點,點A為橢圓C的左頂點,點B為橢圓C的上頂點,且|AB|=
=1(a>b>0)的左、右焦點,點A為橢圓C的左頂點,點B為橢圓C的上頂點,且|AB|=![]() ,△BF1F2為直角三角形.
,△BF1F2為直角三角形.
(1)求橢圓C的方程;
(2)設直線y=kx+2與橢圓交于P、Q兩點,且OP⊥OQ,求實數k的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了解貴州省某州2020屆高三理科生的化學成績的情況,該州教育局組織高三理科生進行了摸底考試,現從參加考試的學生中隨機抽取了100名理科生,,將他們的化學成績(滿分為100分)分為![]()
![]()
![]()
![]()
![]()
![]() 6組,得到如圖所示的頻率分布直方圖.
6組,得到如圖所示的頻率分布直方圖.

(1)求a的值;
(2)記A表示事件“從參加考試的所有理科生中隨機抽取一名學生,該學生的化學成績不低于70分”,試估計事件A發生的概率;
(3)在抽取的100名理科生中,采用分層抽樣的方法從成績在![]() 內的學生中抽取10名,再從這10名學生中隨機抽取4名,記這4名理科生成績在
內的學生中抽取10名,再從這10名學生中隨機抽取4名,記這4名理科生成績在![]() 內的人數為X,求X的分布列與數學期望.
內的人數為X,求X的分布列與數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com