
【題目】已知f(x)=x26x+5. (Ⅰ)求 ![]() 的值;
的值;
(Ⅱ)若x∈[2,6],求f(x)的值域.
【答案】解:(Ⅰ) ![]() f(a)+f(3)=(a26a+5)+(326×3+5)=a26a+1
f(a)+f(3)=(a26a+5)+(326×3+5)=a26a+1
(Ⅱ)解法一:
因為f(x)=x26x+5=(x3)24
又因為x∈[2,6],所以1≤x3≤3,所以0≤(x3)2≤9,
得4≤(x3)24≤5.
所以當x∈[2,6]時,f(x)的值域是[4,5].
解法二:
因為函數f(x)圖象的對稱軸 ![]() ,
,
所以函數f(x)在區間[2,3]是減函數,在區間[3,6]是增函數.
所以x∈[2,6]時, ![]() .
.
又因為f(2)=226×2+5=3,f(6)=626×6+5=5
所以當x∈[2,6]時f(x)的值域是[4,5].
【解析】(Ⅰ)利用二次函數的解析式,直接求 ![]() 的值;(Ⅱ)解法一:利用配方法f(x)=x26x+5=(x3)24,求出x3整體的范圍,然后求解函數的值域即可.
的值;(Ⅱ)解法一:利用配方法f(x)=x26x+5=(x3)24,求出x3整體的范圍,然后求解函數的值域即可.
解法二:求出函數f(x)圖象的對稱軸利用函數的單調性求解函數的值域即可.
【考點精析】解答此題的關鍵在于理解二次函數的性質的相關知識,掌握增減性:當a>0時,對稱軸左邊,y隨x增大而減小;對稱軸右邊,y隨x增大而增大;當a<0時,對稱軸左邊,y隨x增大而增大;對稱軸右邊,y隨x增大而減小.


科目:高中數學 來源: 題型:
【題目】已知a為常數,函數f(x)=xlnx﹣ ![]() ax2 .
ax2 .
(1)當a=0時,求函數f(x)的最小值;
(2)若f(x)有兩個極值點x1 , x2(x1<x2)
①求實數a的取值范圍;
②求證:x1x2>1.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=logax(a>0且a≠1)在區間[1,2]上的最大值與函數g(x)=﹣ ![]() 在區間[1,2]上的最大值互為相反數.
在區間[1,2]上的最大值互為相反數.
(1)求a的值;
(2)若函數F(x)=f(x2﹣mx﹣m)在區間(﹣∞,1﹣ ![]() )上是減函數,求實數m的取值范圍.
)上是減函數,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知正方體ABCD﹣A1B1C1D1的棱長為1,給出下列四個命題: ①對角線AC1被平面A1BD和平面B1 CD1三等分;
②正方體的內切球、與各條棱相切的球、外接球的表面積之比為1:2:3;
③以正方體的頂點為頂點的四面體的體積都是 ![]() ;
;
④正方體與以A為球心,1為半徑的球在該正方體內部部分的體積之比為6:π
其中正確命題的序號為 . 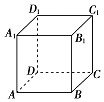
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設實數a∈R,函數 ![]() 是R上的奇函數. (Ⅰ)求實數a的值;
是R上的奇函數. (Ⅰ)求實數a的值;
(Ⅱ)當x∈(1,1)時,求滿足不等式f(1m)+f(1m2)<0的實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=lg ![]() (a>0)為奇函數,函數g(x)=
(a>0)為奇函數,函數g(x)= ![]() +b(b∈R).
+b(b∈R).
(Ⅰ)求a;
(Ⅱ)若b>1,討論方徎g(x)=ln|x|實數根的個數;
(Ⅲ)當x∈[ ![]() ,
, ![]() ]時,關于x的不等式f(1﹣x)≤log(x)有解,求b的取值范圍.
]時,關于x的不等式f(1﹣x)≤log(x)有解,求b的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)= ![]() ,(x>0且a≠1)的圖象經過點(﹣2,3).
,(x>0且a≠1)的圖象經過點(﹣2,3). 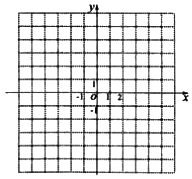
(Ⅰ)求a的值,并在給出的直角坐標系中畫出y=f(x)的圖象;
(Ⅱ)若f(x)在區間(m,m+1)上是單調函數,求m的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com