
【題目】設不等式![]() 表示的平面區別為
表示的平面區別為![]() .區域
.區域![]() 內的動點
內的動點![]() 到直線
到直線![]() 和直線
和直線![]() 的距離之積為2.記點
的距離之積為2.記點![]() 的軌跡為曲線
的軌跡為曲線![]() .過點
.過點![]() 的直線
的直線![]() 與曲線
與曲線![]() 交于
交于![]() 、
、![]() 兩點.
兩點.
(1)求曲線![]() 的方程;
的方程;
(2)若![]() 垂直于
垂直于![]() 軸,
軸,![]() 為曲線
為曲線![]() 上一點,求
上一點,求![]() 的取值范圍;
的取值范圍;
(3)若以線段![]() 為直徑的圓與
為直徑的圓與![]() 軸相切,求直線
軸相切,求直線![]() 的斜率.
的斜率.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)根據“區域![]() 內的動點
內的動點![]() 到直線
到直線![]() 和直線
和直線![]() 的距離之積為
的距離之積為![]() ”列方程,化簡后求得曲線
”列方程,化簡后求得曲線![]() 的方程.
的方程.
(2)求得![]() 兩點的坐標,利用平面向量數量積的坐標運算化簡
兩點的坐標,利用平面向量數量積的坐標運算化簡![]() ,由此求得
,由此求得![]() 的取值范圍.
的取值范圍.
(3)設出直線![]() 的方程,聯立直線
的方程,聯立直線![]() 的方程和曲線
的方程和曲線![]() ,寫出韋達定理.求得以
,寫出韋達定理.求得以![]() 為直徑的圓的圓心和直徑,根據圓與
為直徑的圓的圓心和直徑,根據圓與![]() 軸相切列方程,解方程求得直線
軸相切列方程,解方程求得直線![]() 的斜率.
的斜率.
(1)設![]() ,依題意
,依題意![]() ①,因為
①,因為![]() 滿足不等式
滿足不等式![]() ,所以①可化為
,所以①可化為![]() .
.
(2)將![]() 代入曲線
代入曲線![]() 的方程
的方程![]() ,解得
,解得![]() .取
.取![]() ,設
,設![]() ,因為
,因為![]() 為曲線
為曲線![]() 上一點,故
上一點,故![]() .則
.則![]()
![]()
![]() .即
.即![]() 的取值范圍是
的取值范圍是![]() .
.
(3)設直線![]() 的方程是
的方程是![]() ,
,![]() .聯立
.聯立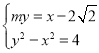 ,消去
,消去![]() 得
得![]() ,所以
,所以![]() .
.
設線段![]() 的中點為
的中點為![]() ,則
,則![]() ,所以
,所以 .
.![]()
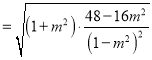 .因為以線段
.因為以線段![]() 為直徑的圓與
為直徑的圓與![]() 軸相切,所以
軸相切,所以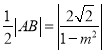 ,即
,即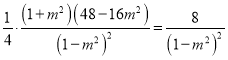 ,化簡得
,化簡得![]() .所以直線
.所以直線![]() 的斜率為
的斜率為![]() .
.


科目:高中數學 來源: 題型:
【題目】(1)已知直線l過點![]() ,它的一個方向向量為
,它的一個方向向量為![]() .
.
①求直線l的方程;
②一組直線![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
![]() 都與直線l平行,它們到直線l的距離依次為d,
都與直線l平行,它們到直線l的距離依次為d,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (
(![]() ),且直線
),且直線![]() 恰好經過原點,試用n表示d的關系式,并求出直線
恰好經過原點,試用n表示d的關系式,并求出直線![]() 的方程(用n、i表示);
的方程(用n、i表示);
(2)在坐標平面上,是否存在一個含有無窮多條直線![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的直線簇,使它同時滿足以下三個條件:①點
的直線簇,使它同時滿足以下三個條件:①點![]() ;②
;②![]() ,其中
,其中![]() 是直線
是直線![]() 的斜率,
的斜率,![]() 和
和![]() 分別為直線
分別為直線![]() 在x軸和y軸上的截距;③
在x軸和y軸上的截距;③![]()
![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(多選題)下列說法正確的是( )
A.橢圓![]() 1上任意一點(非左右頂點)與左右頂點連線的斜率乘積為
1上任意一點(非左右頂點)與左右頂點連線的斜率乘積為![]()
B.過雙曲線![]() 1焦點的弦中最短弦長為
1焦點的弦中最短弦長為![]()
C.拋物線y2=2px上兩點A(x1,y1).B(x2,y2),則弦AB經過拋物線焦點的充要條件為x1x2![]()
D.若直線與圓錐曲線有一個公共點,則該直線和圓錐曲線相切
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某大學為調研學生在![]() ,
, ![]() 兩家餐廳用餐的滿意度,從在
兩家餐廳用餐的滿意度,從在![]() ,
, ![]() 兩家餐廳都用過餐的學生中隨機抽取了100人,每人分別對這兩家餐廳進行評分,滿分均為60分.
兩家餐廳都用過餐的學生中隨機抽取了100人,每人分別對這兩家餐廳進行評分,滿分均為60分.
整理評分數據,將分數以10為組距分成6組: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,得到
,得到![]() 餐廳分數的頻率分布直方圖,和
餐廳分數的頻率分布直方圖,和![]() 餐廳分數的頻數分布表:
餐廳分數的頻數分布表:
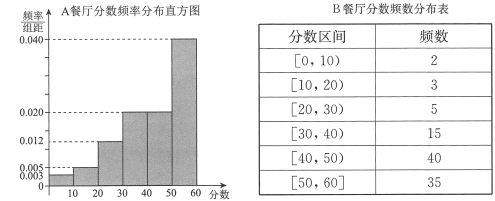
定義學生對餐廳評價的“滿意度指數”如下:
分數 |
|
|
|
滿意度指數 |
|
|
|
(Ⅰ)在抽樣的100人中,求對![]() 餐廳評價“滿意度指數”為0的人數;
餐廳評價“滿意度指數”為0的人數;
(Ⅱ)從該校在, ![]() 兩家餐廳都用過餐的學生中隨機抽取1人進行調查,試估計其對
兩家餐廳都用過餐的學生中隨機抽取1人進行調查,試估計其對![]() 餐廳評價的“滿意度指數”比對
餐廳評價的“滿意度指數”比對![]() 餐廳評價的“滿意度指數”高的概率;
餐廳評價的“滿意度指數”高的概率;
(Ⅲ)如果從![]() ,
, ![]() 兩家餐廳中選擇一家用餐,你會選擇哪一家?說明理由.
兩家餐廳中選擇一家用餐,你會選擇哪一家?說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如果你留心使會發現,汽車前燈后的反射鏡呈拋物線的形狀,把拋物線沿它的對稱軸旋轉一周,就會形成一個拋物面.這種拋物面形狀,正是我們熟悉的汽車前燈的反射鏡形狀,這種形狀使車燈既能夠發出明亮的、照射很遠的平行光束,又能發出較暗的,照射近距離的光線.我們都知道常規的前照燈主要是由燈泡、反射鏡和透鏡三部分組成,明亮的光束,是由位于拋物面形狀反射鏡焦點的光源射出的,燈泡位于拋物面的焦點上,燈泡發出的光經拋物面反射鏡反射形成平行光束,再經過配光鏡的散射、偏轉作用,以達到照亮路面的效果,這樣的燈光我們通常稱為遠光燈:而較暗的光線,不是由反射鏡焦點的光源射出的,光線的行進與拋物線的對稱軸不平行,光線只能向上和向下照射,所以照射距離并不遠,如果把向上射出的光線遮住.車燈就只能發出向下的、射的很近的光線了.請用數學的語言歸納表達遠光燈的照明原理,并證明.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知雙曲線C:![]() (a>0,b>0)的離心率為
(a>0,b>0)的離心率為![]() ,且
,且![]()
(1)求雙曲線C的方程;
(2)已知直線![]() 與雙曲線C交于不同的兩點A,B且線段AB的中點在圓
與雙曲線C交于不同的兩點A,B且線段AB的中點在圓![]() 上,求m的值
上,求m的值
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了選拔學生參加全市中學生物理競賽,學校先從高三年級選取60名同學進行競賽預選賽,將參加預選賽的學生成績(單位:分)按范圍![]() ,
,![]() ,
,![]() ,
,![]() 分組,得到的頻率分布直方圖如圖:
分組,得到的頻率分布直方圖如圖:

(1)計算這次預選賽的平均成績(同一組中的數據用該組區間的中點值作代表);
(2)若對得分在前![]() 的學生進行校內獎勵,估計獲獎分數線;
的學生進行校內獎勵,估計獲獎分數線;
(3)若這60名學生中男女生比例為![]() ,成績不低于60分評估為“成績良好”,否則評估為“成績一般”,試完成下面
,成績不低于60分評估為“成績良好”,否則評估為“成績一般”,試完成下面![]() 列聯表,是否有
列聯表,是否有![]() 的把握認為“成績良好”與“性別”有關?
的把握認為“成績良好”與“性別”有關?
成績良好 | 成績一般 | 合計 | |
男生 | |||
女生 | |||
合計 |
附:![]() ,
,![]()
臨界值表:
| 0.10 | 0.05 | 0.010 |
| 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國古代數學名著《九章算術》中記載了有關特殊幾何體的定義:陽馬指底面為矩形,一側棱垂直于底面的四棱錐,塹堵指底面是直角三角形,且側棱垂直于底面的三棱柱.
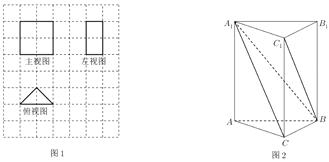
(1)某塹堵的三視圖,如圖1,網格中的每個小正方形的邊長為1,求該塹堵的體積;
(2)在塹堵![]() 中,如圖2,
中,如圖2,![]() ,若
,若![]() ,當陽馬
,當陽馬![]() 的體積最大時,求二面角
的體積最大時,求二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知雙曲線![]() =1(a>0,b>0)的左、右焦點分別為F1,F2,點O為雙曲線的中心,點P在雙曲線右支上,△PF1F2內切圓的圓心為Q,圓Q與x軸相切于點A,過F2作直線PQ的垂線,垂足為B,則下列結論成立的是( )
=1(a>0,b>0)的左、右焦點分別為F1,F2,點O為雙曲線的中心,點P在雙曲線右支上,△PF1F2內切圓的圓心為Q,圓Q與x軸相切于點A,過F2作直線PQ的垂線,垂足為B,則下列結論成立的是( )
A. |OA|>|OB|B. |OA|<|OB|
C. |OA|=|OB|D. |OA|與|OB|大小關系不確定
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com