
某校在一次趣味運動會的頒獎儀式上,高一、高二、高三各代表隊人數分別為120人、120人、 人.為了活躍氣氛,大會組委會在頒獎過程中穿插抽獎活動,并用分層抽樣的方法從三個代表隊中共抽取20人在前排就坐,其中高二代表隊有6人.
人.為了活躍氣氛,大會組委會在頒獎過程中穿插抽獎活動,并用分層抽樣的方法從三個代表隊中共抽取20人在前排就坐,其中高二代表隊有6人.
(1)求 的值;
的值;
(2)把在前排就坐的高二代表隊6人分別記為 ,現隨機從中抽取2人上臺抽獎,
,現隨機從中抽取2人上臺抽獎,
求 和
和 至少有一人上臺抽獎的概率;
至少有一人上臺抽獎的概率;
(3)抽獎活動的規則是:代表通過操作按鍵使電腦自動產生兩個 之間的均勻隨機數
之間的均勻隨機數 ,并按如右所示的程序框圖執行.若電腦顯示“中獎”,則該代表中獎;若電腦顯示“謝謝”,則不中獎,求該代表中獎的概率.
,并按如右所示的程序框圖執行.若電腦顯示“中獎”,則該代表中獎;若電腦顯示“謝謝”,則不中獎,求該代表中獎的概率.
(1)160;(2)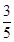 ;(3)
;(3)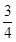
解析試題分析:(1)分層抽樣是安比例抽取,所以根據比例相等列式計算。(2)屬古典概型概率,用例舉法將所有情況一一例舉出來計算基本事件總數,再將符合要求的事件找出來計算出基本事件數,根據古典概型概率公式求其概率。(3)屬幾何概型概率,數形結合需畫出圖像分析。
試題解析:解:(1)依題意,由 ,解得
,解得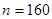 2分
2分
(2)記事件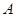 為“
為“ 和
和 至少有一人上臺抽獎”, 3分
至少有一人上臺抽獎”, 3分
從高二代表隊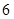 人中抽取
人中抽取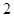 人上臺抽獎的所有基本事件列舉如下:
人上臺抽獎的所有基本事件列舉如下: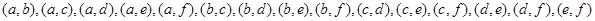 共15種可能, 5分
共15種可能, 5分
其中事件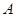 包含的基本事件有9種 6分
包含的基本事件有9種 6分
所以 7分
7分
(3)記事件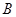 為“該代表中獎”如圖,
為“該代表中獎”如圖,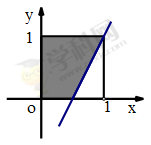
 所表示的平面區域是以
所表示的平面區域是以 為邊的正方形,而中獎所表示的平面區域為陰影部分 9分
為邊的正方形,而中獎所表示的平面區域為陰影部分 9分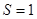 ,陰影部分面積
,陰影部分面積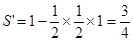 11分
11分
所以該代表中獎的概率為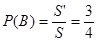 12分
12分
考點:1分層抽樣;2古典概型概率;3幾何概型概率;4二元一次不等式表示平面區域。


 53隨堂測系列答案
53隨堂測系列答案科目:高中數學 來源: 題型:解答題
在甲、乙等6個單位參加的一次“唱讀講傳”演出活動中,每個單位的節目集中安排在一起.若采用抽簽的方式隨機確定各單位的演出順序(序號為1,2,…,6),求:
(1)甲、乙兩單位的演出序號均為偶數的概率;
(2)甲、乙兩單位的演出序號不相鄰的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某校高三(1)班的一次數學測試成績的莖葉圖和頻率分布直方圖都受到不同程度的破壞,可見部分如下:
試根據圖表中的信息解答下列問題:
(1)求全班的學生人數及分數在[70,80)之間的頻數;
(2)為快速了解學生的答題情況,老師按分層抽樣的方法從位于[70,80),[80,90)和[90,100]分數段的試卷中抽取8份進行分析,再從中任選3人進行交流,求交流的學生中,成績位于[70,80)分數段的人數X的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某車間共有12名工人,隨機抽取6名,他們某日加工零件個數的莖葉圖如圖所示,其中莖為十位數,葉為個位數.
(1)根據莖葉圖計算樣本均值;
(2)日加工零件個數大于樣本均值的工人為優秀工人.根據莖葉圖推斷該車間12名工人中有幾名優秀工人?
(3)從該車間12名工人中,任取2人,求恰有1名優秀工人的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
盒子中裝有四張大小形狀均相同的卡片,卡片上分別標有數字-1,0,1,2.稱“從盒中隨機抽取一張,記下卡片上的數字后并放回”為一次試驗(設每次試驗的結果互不影響).
(1)在一次試驗中,求卡片上的數字為正數的概率;
(2)在四次試驗中,求至少有兩次卡片上的數字都為正數的概率;
(3)在兩次試驗中,記卡片上的數字分別為X,η,試求隨機變量X=X·η的分布列與數學期望E(X).
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
為了調查學生的視力情況,隨機抽查了一部分學生的視力,將調查結果分組,分組區間為 ,經過數據處理,得到如下頻率分布表
,經過數據處理,得到如下頻率分布表
| 分組 | 頻數 | 頻率 |
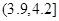 | 3 | 0.06 |
 | 6 | 0.12 |
 | 25 | 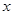 |
 | 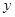 | 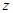 |
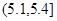 | 2 | 0.04 |
| 合計 | 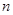 | 1.00 |
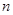 ,
,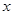 ,
,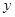 ,
,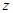 的值
的值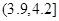 和
和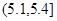 的所有同學中隨機抽取兩人,求兩人視力差的絕對值低于
的所有同學中隨機抽取兩人,求兩人視力差的絕對值低于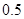 的概率
的概率查看答案和解析>>
科目:高中數學 來源: 題型:解答題
為拉動經濟增長,某市決定新建一批基礎設施工程、民生工程和產業建設工程三類,這三類工程所含項目個數分別占總數的 ,
, ,
, ,現在3名工人獨立地從中任意一個項目參與建設.
,現在3名工人獨立地從中任意一個項目參與建設.
(1)求他們選擇的項目所屬類別互不相同的概率.
(2)記X為3人中選擇的項目所屬于基礎設施工程或產業建設工程的人數,求X的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
一個盒子里裝有7張卡片,其中有紅色卡片4張,編號分別為1,2,3,4;白色卡片3張,編號分別為2,3,4.從盒子中任取4張卡片(假設取到任何一張卡片的可能性相同).
(1)求取出的4張卡片中,含有編號為3的卡片的概率;
(2)在取出的4張卡片中,紅色卡片編號的最大值設為X,求隨機變量X的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某學生參加某高校的自主招生考試,須依次參加A,B,C,D,E五項考試,如果前四項中有兩項不合格或第五項不合格,則該考生就被淘汰,考試即結束;考生未被淘汰時,一定繼續參加后面的考試.已知每一項測試都是相互獨立的,該生參加A,B,C,D四項考試不合格的概率均為 ,參加第五項不合格的概率為
,參加第五項不合格的概率為 .
.
(1)求該生被錄取的概率;
(2)記該生參加考試的項數為X,求X的分布列和期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com