
【題目】在△ABC中,內角A,B,C所對的邊分別為a,b,c,已知b+c=2acosB.
(1)證明:A=2B;
(2)若cosB= ![]() ,求cosC的值.
,求cosC的值.
【答案】
(1)
證明:∵b+c=2acosB,
∴sinB+sinC=2sinAcosB,
∵sinC=sin(A+B)=sinAcosB+cosAsinB,
∴sinB=sinAcosB﹣cosAsinB=sin(A﹣B),由A,B∈(0,π),
∴0<A﹣B<π,∴B=A﹣B,或B=π﹣(A﹣B),化為A=2B,或A=π(舍去).
∴A=2B.
(2)
解:cosB= ![]() ,∴sinB=
,∴sinB= ![]() =
= ![]() .
.
cosA=cos2B=2cos2B﹣1= ![]() ,sinA=
,sinA= ![]() =
= ![]() .
.
∴cosC=﹣cos(A+B)=﹣cosAcosB+sinAsinB= ![]() =
= ![]() .
.
【解析】(1)由b+c=2acosB,利用正弦定理可得:sinB+sinC=2sinAcosB,而sinC=sin(A+B)=sinAcosB+cosAsinB,代入化簡可得:sinB=sin(A﹣B),由A,B∈(0,π),可得0<A﹣B<π,即可證明.(2)cosB= ![]() ,可得sinB=
,可得sinB= ![]() .cosA=cos2B=2cos2B﹣1,sinA=
.cosA=cos2B=2cos2B﹣1,sinA= ![]() .利用cosC=﹣cos(A+B)=﹣cosAcosB+sinAsinB即可得出.本題考查了正弦定理、和差公式、倍角公式、同角三角函數基本關系式、誘導公式,考查了推理能力與計算能力,屬于中檔題.
.利用cosC=﹣cos(A+B)=﹣cosAcosB+sinAsinB即可得出.本題考查了正弦定理、和差公式、倍角公式、同角三角函數基本關系式、誘導公式,考查了推理能力與計算能力,屬于中檔題.
【考點精析】掌握正弦定理的定義是解答本題的根本,需要知道正弦定理:![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】如圖,以坐標原點O為圓心的單位圓與x軸正半軸相交于點A,點B,P在單位圓上,且![]()
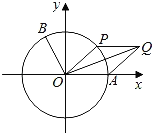
(1)求![]() 的值;
的值;
(2)設![]()
![]() ,四邊形
,四邊形![]() 的面積為
的面積為![]() ,
,![]() ,求
,求![]() 的最值及此時
的最值及此時![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x2+bx,則“b<0”是“f(f(x))的最小值與f(x)的最小值相等”的( )
A.充分不必要條件
B.必要不充分條件
C.充分必要條件
D.既不充分也不必要條件
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓心在![]() 軸上的圓
軸上的圓![]() 與直線
與直線![]() 切于點
切于點![]() .圓
.圓![]() :
: ![]() .
.
(1)求圓![]() 的標準方程;
的標準方程;
(2)已知![]() ,圓
,圓![]() 與
與![]() 軸相交于兩點
軸相交于兩點![]() (點
(點![]() 在點
在點![]() 的右側).過點
的右側).過點![]() 任作一條傾斜角不為0的直線與圓
任作一條傾斜角不為0的直線與圓![]() 相交于
相交于![]() 兩點.問:是否存在實數
兩點.問:是否存在實數![]() ,使得
,使得![]() ?若存在,求出實數
?若存在,求出實數![]() 的值,若不存在,請說明理由.
的值,若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知長方形ABCD中,AB=2AD,M為DC的中點,將△ADM沿AM折起,使得平面ADM⊥平面ABCM. 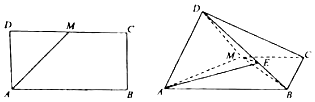
(1)求證:AD⊥BM;
(2)若 ![]() =2
=2 ![]() ,求二面角E﹣AM﹣D的正弦值.
,求二面角E﹣AM﹣D的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f( ![]() )=﹣
)=﹣ ![]() x3+
x3+ ![]() x2﹣m,g(x)=﹣
x2﹣m,g(x)=﹣ ![]() x3+mx2+(a+1)x+2xcosx﹣m.
x3+mx2+(a+1)x+2xcosx﹣m.
(1)若曲線y=f(x)僅在兩個不同的點A(x1 , f(x1)),B(x1 , f(x2))處的切線都經過點(2,t),求證:t=3m﹣8,或t=﹣ ![]() m3+
m3+ ![]() m2﹣m.
m2﹣m.
(2)當x∈[0,1]時,若f(x)≥g(x)恒成立,求a的取值范圍.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com