【題目】如圖，已知長方形ABCD中，AB=2AD，M為DC的中點，將△ADM沿AM折起，使得平面ADM⊥平面ABCM．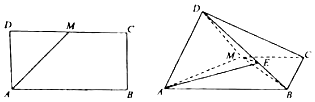 
（1）求證：AD⊥BM；
（2）若 
=2 
，求二面角E﹣AM﹣D的正弦值．
【答案】
（1）證明：長方形ABCD中，設AB=2，AD=1，M為DC的中點
則AM=BM= 
，∴AM2+BM2=AB2，∴BM⊥AM
∵平面ADM⊥平面ABCM，平面ADM∩平面ABCM=AM，BM平面ABCM
∴BM⊥平面ADM
∵AD平面ADM，∴AD⊥BM
（2）解：建立如圖所示的直角坐標系，
∵ 
=2 
，設AB=2，AD=1，
∴A（ 
，0，0），M（﹣ ，0，0），B（﹣ ， ，0），D（0，0， ），
則平面AMD的一個法向量 
=（0，1，0），
=（ 
， 
， ）， 
=（﹣ ，0，0），
設AME的一個法向量 
=（x，y，z），
則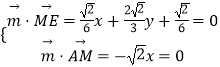 
，取y=1，得 =（0，1，﹣4），
設二面角E﹣AM﹣D的平面角為θ，
則cosθ= 
= 
，sinθ= 
= 
，
∴二面角E﹣AM﹣D的正弦值為 ．
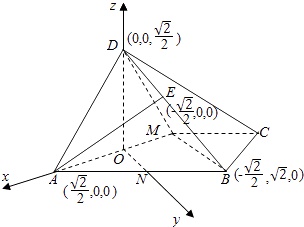
【解析】（1）先證明BM⊥AM，再利用平面ADM⊥平面ABCM，證明BM⊥平面ADM，從而可得AD⊥BM．（2）建立直角坐標系，求出平面AMD、平面AME的一個法向量，利用向量的夾角公式，即可得出二面角E﹣AM﹣D的正弦值．
步步高達標卷系列答案科目：高中數學 來源： 題型：
【題目】已知圓M：x2+y2﹣2ay=0（a＞0）截直線x+y=0所得線段的長度是2 
，則圓M與圓N：（x﹣1）2+（y﹣1）2=1的位置關系是（ ）
A.內切
B.相交
C.外切
D.相離
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在△ABC中，內角A，B，C所對的邊分別為a，b，c，已知b+c=2acosB．
（1）證明：A=2B；
（2）若cosB= 
，求cosC的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖,M是矩形ABCD的邊CD上的一點,AC與BM交于點N,BN=
BM.
(1)求證:M是CD的中點;
(2)若AB=2,BC=1,H是BM上異于點B的一動點,求
的最小值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=x2e2x+m|x|ex+1（m∈R）有四個零點，則m的取值范圍為（ ）
A.（﹣∞，﹣e﹣ 
）
B.（﹣∞，e+ ）
C.（﹣e﹣ ，﹣2）
D.（﹣∞，﹣ ）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=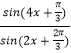 
的圖象與g（x）的圖象關于直線x= 
對稱，則g（x）的圖象的一個對稱中心為（ ）
A.（ 
，0）
B.（ 
，0）
C.（ 
，0）
D.（ 
，0）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f(x)=|x﹣a|，g（x）=x2+2ax+1（a為正實數），滿足f(0)=g(0)；
函數F(x)=f(x)+g(x)+b定義域為D．
（1）求a的值；
（2）若存在x0∈D，使F(x0)=x0成立，求實數b的取值范圍；
（3）若n為正整數，證明：
＜4．
（參考數據：lg3=0.3010， 
=0.1342，
=0.0281，
=0.0038）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓Г： 
（a＞b＞0）的左、右焦點分別為F1 ， F2 ， 離心率為 
，F2與橢圓上點的連線的中最短線段的長為 
﹣1．
（1）求橢圓Г的標準方程；
（2）已知Г上存在一點P，使得直線PF1 ， PF2分別交橢圓Г于A，B，若 
=2 
， 
=λ 
（λ＞0），求λ的值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
