
(本題滿分14分)定義在D上的函數 ,如果滿足;對任意
,如果滿足;對任意 ,存在常數
,存在常數 ,都有
,都有 成立,則稱
成立,則稱 是D上的有界函數,其中M稱為函數
是D上的有界函數,其中M稱為函數 的上界。
的上界。
已知函數 ,
,
(1)當 時,求函數
時,求函數 在
在 上的值域,并判斷函數
上的值域,并判斷函數 在
在 上是否為有界函數,請說明理由;
上是否為有界函數,請說明理由;
(2)若函數 在
在 上是以3為上界函數值,求實數
上是以3為上界函數值,求實數 的取值范圍;
的取值范圍;
(3)若 ,求函數
,求函數 在
在 上的上界T的取值范圍。
上的上界T的取值范圍。
解:(1)當 時,
時, .
.
∵ 在
在 上遞增,所以
上遞增,所以 ,
,
即 在
在 上的值域為
上的值域為 . …………………………………2分
. …………………………………2分
故不存在常數 ,使
,使 成立.
成立.
所以函數 在
在 上不是有界函數. ……………………………………4分
上不是有界函數. ……………………………………4分
(2)∵函數 在
在 上是以3為上界的有界函數,
上是以3為上界的有界函數,

 在
在 上恒成立.
上恒成立.  ,
,
 在
在 上恒成立.
上恒成立.
 ……………………………6分
……………………………6分
設 ,
, ,
, .
.
由
 ,得
,得 .設
.設 ,則
,則
 ,
, ,
,
所以 在
在 上遞增,
上遞增, 在
在 上遞減.
上遞減.
 在
在 上的最大值為
上的最大值為 ,
, 在
在 上的最小值為
上的最小值為 .
.
所以實數 的取值范圍為
的取值范圍為 . …………………………………………… 9分
. …………………………………………… 9分
(3))方法一: ,
, .
.
∵ m>0 , ,
,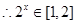 .
.
∴
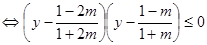 ,
,
∵
∴ .
…………………………………………11分
.
…………………………………………11分
① 當 ,即
,即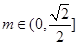 時,
時,
 ,此時
,此時 ;
;
② 當 ,即
,即 時,
時,
 ,此時
,此時 .
.
綜上所述,當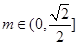 時,
時, 的取值范圍是
的取值范圍是 ;當
;當 時,
時, 的取值范圍是
的取值范圍是 ………………………………………………………14分
………………………………………………………14分
方法二:  .
.
令 ,因為
,因為 ,所以
,所以 .
.
 .
.
因為 在
在 上是減函數,所以
上是減函數,所以 .…………………11分
.…………………11分
又因為函數 在
在 上的上界是
上的上界是 ,所以
,所以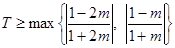 .
.
當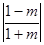

 時,
時, ,
,

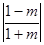
 ;
;
當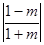

 時,
時, ,
,


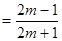 .……………………14分
.……………………14分
【解析】略


科目:高中數學 來源:2011年甘肅省高一上學期期中考試數學 題型:解答題
(本題滿分14分)某租賃公司擁有汽車100輛.當每輛車的月租金為3000元時,可全部租出.當每輛車的月租金每增加50元時,未租出的車將會增加一輛.租出的車每輛每月需要維護費150元,未租出的車每輛每月需要維護費50元.
(1)當每輛車的月租金定為3600元時,能租出多少輛車?
(2)當每輛車的月租金定為多少元時,租賃公司的月收益最大?最大月收益是多少?
查看答案和解析>>
科目:高中數學 來源:2010-2011學年江西省六校高三聯考數學理卷 題型:解答題
((本題滿分14分)
已知橢圓的兩個焦點 ,且橢圓短軸的兩個端點與
,且橢圓短軸的兩個端點與 構成正三角形.
構成正三角形.
(1)求橢圓的方程;
(2)過點(1,0)且與坐標軸不平行的直線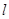 與橢圓交于不同兩點P、Q,若在
與橢圓交于不同兩點P、Q,若在 軸上存在定點E(
軸上存在定點E( ,0),使
,0),使 恒為定值,求
恒為定值,求 的值.
的值.
查看答案和解析>>
科目:高中數學 來源:2010-2011學年廣東省惠州市高三第三次調研考試數學文卷 題型:解答題
(本題滿分14分)
已知動圓過定點 ,且與定直線
,且與定直線 相切.
相切.
(1)求動圓圓心的軌跡 的方程;
的方程;
(2)若 是軌跡
是軌跡 的動弦,且
的動弦,且 過
過 , 分別以
, 分別以 、
、 為切點作軌跡
為切點作軌跡 的切線,設兩切線交點為
的切線,設兩切線交點為 ,證明:
,證明: .
.
查看答案和解析>>
科目:高中數學 來源:2013屆廣東省高二第一學期期末考試文科數學 題型:解答題
(本題滿分14分)
已知動圓過定點P(1,0)且與定直線 相切,點C在
相切,點C在 上.
上.
(Ⅰ)求動圓圓心M的軌跡方程;
(Ⅱ)設過點P且斜率為 的直線與曲線交于A、B兩點.問直線
的直線與曲線交于A、B兩點.問直線 上是否存在點C ,使得
上是否存在點C ,使得 是以
是以 為直角的直角三角形?如果存在,求出點C的坐標;若不能,請說明理由.
為直角的直角三角形?如果存在,求出點C的坐標;若不能,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com