
【題目】已知函數f(x)=a﹣ ![]() 為奇函數.
為奇函數.
(1)求a的值;
(2)試判斷函數f(x)在(﹣∞,+∞)上的單調性,并證明你的結論;
(3)若對任意的t∈R,不等式f[t2﹣(m﹣2)t]+f(t2﹣m+1)>0恒成立,求實數m的取值范圍.
【答案】
(1)解:由于函數f(x)為奇函數,所以f(﹣x)=﹣f(x);
∴a﹣ ![]() =﹣a+
=﹣a+ ![]() ;
;
∴2a= ![]() ;
;
∴a=1
(2)解:任意x1,x2∈R,且x1<x2;
f(x1)﹣f(x2)=1﹣ ![]() ﹣1+
﹣1+ ![]() ;
;
= ![]() <0;
<0;
∵x1<x2∴0< ![]() <
< ![]()
∴ ![]() >0,
>0,
所以,f(x1)<f(x2);
則f(x)為R上的單調遞增函數
(3)解:因為f(x)=1﹣ ![]() 為奇函數,且在R上為增函數;
為奇函數,且在R上為增函數;
所以由f(t2﹣(m﹣2)t)+f(t2﹣m+1)>0恒成立,
得到:t2﹣(m﹣2)t>m﹣1﹣t2 對t∈R恒成立;
化簡后:2t2﹣(m﹣2)t﹣m+1>0;
所以△=(m﹣2)2+8(m﹣1)<0;
∴﹣2﹣2 ![]() <m<﹣2+2
<m<﹣2+2 ![]() ;
;
故m的取值范圍為:(﹣2﹣2 ![]() ,﹣2+2
,﹣2+2 ![]() )
)
【解析】(1)直接利用奇函數的定義f(﹣x)=f(x),可求出a值;(2)直接利用函數的單調性定義證明即可;(3)利用奇函數與單調性直接轉化為t2﹣(m﹣2)t>m﹣1﹣t2 對t∈R恒成立,從而求出m的取值范圍.
【考點精析】通過靈活運用奇偶性與單調性的綜合,掌握奇函數在關于原點對稱的區間上有相同的單調性;偶函數在關于原點對稱的區間上有相反的單調性即可以解答此題.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ax2﹣x+2a﹣1(a>0).
(1)若f(x)在區間[1,2]為單調增函數,求a的取值范圍;
(2)設函數f(x)在區間[1,2]上的最小值為g(a),求g(a)的表達式;
(3)設函數 ![]() ,若對任意x1 , x2∈[1,2],不等式f(x1)≥h(x2)恒成立,求實數a的取值范圍.
,若對任意x1 , x2∈[1,2],不等式f(x1)≥h(x2)恒成立,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,橢圓![]() 的離心率為
的離心率為![]() ,頂點為
,頂點為![]() ,且
,且![]() .
.
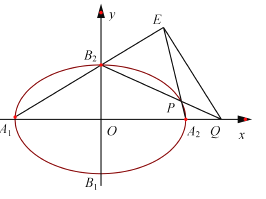
(1)求橢圓![]() 的方程;
的方程;
(2)![]() 是橢圓
是橢圓![]() 上除頂點外的任意點,直線
上除頂點外的任意點,直線![]() 交
交![]() 軸于點
軸于點![]() ,直線
,直線![]() 交
交![]() 于點
于點![]() .設
.設![]() 的斜率為
的斜率為![]() ,
, ![]() 的斜率為
的斜率為![]() ,試問
,試問![]() 是否為定值?并說明理由.
是否為定值?并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知集合A={x| ![]() >0},集合B={x|y=lg(﹣x2+3x+28)},集合C={x|m+1≤x≤2m﹣1}.
>0},集合B={x|y=lg(﹣x2+3x+28)},集合C={x|m+1≤x≤2m﹣1}.
(1)求(RA)∩B;
(2)若B∪C=B,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】本市某玩具生產公司根據市場調查分析,決定調整產品生產方案,準備每天生產![]() ,
, ![]() ,
, ![]() 三種玩具共100個,且
三種玩具共100個,且![]() 種玩具至少生產20個,每天生產時間不超過10小時,已知生產這些玩具每個所需工時(分鐘)和所獲利潤如表:
種玩具至少生產20個,每天生產時間不超過10小時,已知生產這些玩具每個所需工時(分鐘)和所獲利潤如表:
玩具名稱 |
|
|
|
工時(分鐘) | 5 | 7 | 4 |
利潤(元) | 5 | 6 | 3 |
(Ⅰ)用每天生產![]() 種玩具個數
種玩具個數![]() 與
與![]() 種玩具
種玩具![]() 表示每天的利潤
表示每天的利潤![]() (元);
(元);
(Ⅱ)怎樣分配生產任務才能使每天的利潤最大,最大利潤是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=( ![]() )x的圖象與函數g(x)的圖象關于直線y=x對稱,令h(x)=g(1﹣|x|),則關于h(x)有下列命題:
)x的圖象與函數g(x)的圖象關于直線y=x對稱,令h(x)=g(1﹣|x|),則關于h(x)有下列命題:
①h(x)的圖象關于原點對稱;
②h(x)為偶函數;
③h(x)的最小值為0;
④h(x)在(0,1)上為減函數.
其中正確命題的序號為: .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com