
關于 的函數
的函數 ,有下列結論:
,有下列結論:
①、該函數的定義域是 ; ②、該函數是奇函數;
; ②、該函數是奇函數;
③、該函數的最小值為 ;
;
④、當 時
時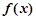 為增函數,當
為增函數,當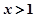 時
時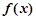 為減函數;
為減函數;
其中,所有正確結論的序號是 。
①④
解析試題分析: :①函數f(x)的定義域是(0,+∞),令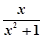 >0,解得x>0,故定義域是(0,+∞),命題正確;
>0,解得x>0,故定義域是(0,+∞),命題正確;
②函數f(x)是奇函數,由①知,定義域不關于原點對稱,故不是奇函數,命題不正確;
③函數f(x)的最大值為-lg2,因為f(x)= 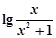 =lg
=lg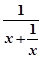 ≤lg
≤lg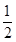 =-lg2,最大值是-lg2,故命題不正確;
=-lg2,最大值是-lg2,故命題不正確;
④當0<x<1時,函數f(x)是增函數;當x>1時,函數f(x)是減函數,命題正確,因為f′(x)=lg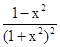 ,令導數大于0,可解得0<x<1,令導數大于0,得x>1,故命題正確.綜上,①④正確,故答案為:①④
,令導數大于0,可解得0<x<1,令導數大于0,得x>1,故命題正確.綜上,①④正確,故答案為:①④
考點:本題主要考查了函數定義域、最值、單調性和奇偶性,同時考查了推理論證的能力以及計算論證的能力,屬于中檔題.
點評:解決該試題的關鍵是①根據對數函數的真數大于0,建立關系式解之驗證定義域即可;②函數f(x)是奇函數,利用奇函數的定義進行判斷;③函數f(x)的最大值為-lg2,利用基本不等式與對數的運算性質求出最值;④求出導數,解出單調區間,驗證即可.


科目:高中數學 來源: 題型:填空題
某同學在研究函數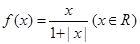 時,分別給出下面幾個結論:
時,分別給出下面幾個結論:
①等式 對
對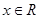 恒成立; ②函數
恒成立; ②函數 的值域為
的值域為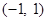 ;
;
③若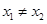 ,則一定有
,則一定有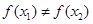 ; ④函數
; ④函數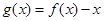 在
在 上有三個零點。 其中正確結論的序號有____________.
上有三個零點。 其中正確結論的序號有____________.
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
下列5個判斷:
①若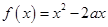 在
在 上增函數,則
上增函數,則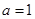 ;
;
②函數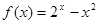 只有兩個零點;
只有兩個零點;
③函數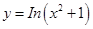 的值域是
的值域是 ;
;
④函數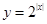 的最小值是1;
的最小值是1;
⑤在同一坐標系中函數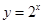 與
與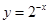 的圖像關于
的圖像關于 軸對稱。
軸對稱。
其中正確命題的序號是 。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com