
【題目】深受廣大球迷喜愛的某支歐洲足球隊.在對球員的使用上總是進行數據分析,為了考察甲球員對球隊的貢獻,現作如下數據統計:
球隊勝 | 球隊負 | 總計 | |
甲參加 |
|
|
|
甲未參加 |
|
|
|
總計 |
|
|
|
(1)求![]() 的值,據此能否有
的值,據此能否有![]() 的把握認為球隊勝利與甲球員參賽有關;
的把握認為球隊勝利與甲球員參賽有關;
(2)根據以往的數據統計,乙球員能夠勝任前鋒、中鋒、后衛以及守門員四個位置,且出場率分別為:![]() ,當出任前鋒、中鋒、后衛以及守門員時,球隊輸球的概率依次為:
,當出任前鋒、中鋒、后衛以及守門員時,球隊輸球的概率依次為:![]() .則:
.則:
1)當他參加比賽時,求球隊某場比賽輸球的概率;
2)當他參加比賽時,在球隊輸了某場比賽的條件下,求乙球員擔當前鋒的概率;
3)如果你是教練員,應用概率統計有關知識.該如何使用乙球員?
附表及公式:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]() .
.
【答案】(1)![]() 有
有![]() 的把握(2)1)0.32, 2)0.32, 3)多讓乙球員擔當守門員,
的把握(2)1)0.32, 2)0.32, 3)多讓乙球員擔當守門員,
【解析】分析:(1)直接根據2×2列聯表求![]() 的值,利用
的值,利用![]() 公式求出
公式求出![]() 的值,再判斷有
的值,再判斷有![]() 的把握認為球隊勝利與甲球員參賽有關.(2)1)利用互斥事件的概率公式求球隊某場比賽輸球的概率;2)利用條件概率求乙球員擔當前鋒的概率;3)因為
的把握認為球隊勝利與甲球員參賽有關.(2)1)利用互斥事件的概率公式求球隊某場比賽輸球的概率;2)利用條件概率求乙球員擔當前鋒的概率;3)因為![]() ,所以應該多讓乙球員擔當守門員,來擴大贏球場次.
,所以應該多讓乙球員擔當守門員,來擴大贏球場次.
詳解:(1)![]() ,
,
![]() 有
有![]() 的把握認為球隊勝利與甲球員參賽有關.
的把握認為球隊勝利與甲球員參賽有關.
(2)1)設![]() 表示“乙球員擔當前鋒”;
表示“乙球員擔當前鋒”;![]() 表示“乙球員擔當中鋒 ”;
表示“乙球員擔當中鋒 ”;![]() 表示“乙球員擔當后衛”;
表示“乙球員擔當后衛”;![]() 表示“乙球員擔當守門員”;
表示“乙球員擔當守門員”;![]() 表示“球隊輸掉某場比賽”,則
表示“球隊輸掉某場比賽”,則![]()
![]() .
.
2)![]() .
.
3)因為![]() ,所以應該多讓乙球員擔當守門員,來擴大贏球場次.
,所以應該多讓乙球員擔當守門員,來擴大贏球場次.


科目:高中數學 來源: 題型:
【題目】某港口O要將一件重要物品用小艇送到一艘正在航行的輪船上,在小艇出發時,輪船位于港口的O北偏西30°且與該港口相距20海里的A處,并正以30海里/小時的航行速度沿正東方向勻速行駛.假設該小艇沿直線方向以v海里/小時的航行速度勻速行駛,經過t小時與輪船相遇.
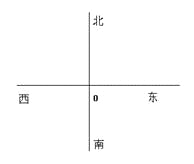
(I)若希望相遇時小艇的航行距離最小,則小艇航行速度的大小應為多少?
(II)為保證小艇在30分鐘內(含30分鐘)能與輪船相遇,試確定小艇航行速度的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知點![]() 是圓心為
是圓心為![]() 半徑為
半徑為![]() 的半圓弧上從點
的半圓弧上從點![]() 數起的第一個三等分點,點
數起的第一個三等分點,點![]() 是圓心為
是圓心為![]() 半徑為
半徑為![]() 的半圓弧的中點,
的半圓弧的中點,![]() 、
、![]() 分別是兩個半圓的直徑,
分別是兩個半圓的直徑,![]() ,直線
,直線![]() 與兩個半圓所在的平面均垂直,直線
與兩個半圓所在的平面均垂直,直線![]() 、
、![]() 共面.
共面.

(1)求三棱錐![]() 的體積;
的體積;
(2)求直線![]() 與
與![]() 所成角的余弦值.
所成角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,左、右焦點分別為
,左、右焦點分別為![]() ,且
,且![]() ,
,
⊙![]() 與該橢圓有且只有一個公共點.
與該橢圓有且只有一個公共點.
(1)求橢圓標準方程;
(2)過點![]() 的直線與⊙
的直線與⊙![]() 相切,且與橢圓相交于
相切,且與橢圓相交于![]() 兩點,求證:
兩點,求證:![]() ;
;
(3)過點![]() 的直線
的直線![]() 與⊙
與⊙![]() 相切,且與橢圓相交于
相切,且與橢圓相交于![]() 兩點,試探究
兩點,試探究![]() 的數量關系.
的數量關系.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(題文)如圖所示的某種容器的體積為![]() ,它是由圓錐和圓柱兩部分連接而成,圓柱與圓錐的底面半徑都為
,它是由圓錐和圓柱兩部分連接而成,圓柱與圓錐的底面半徑都為![]() .圓錐的高為
.圓錐的高為![]() ,母線與底面所成的角為
,母線與底面所成的角為![]() ;圓柱的高為
;圓柱的高為![]() ,已知圓柱底面的造價為
,已知圓柱底面的造價為![]() 元
元![]() ,圓柱側面造價為
,圓柱側面造價為![]() 元
元![]() ,圓錐側面造價為
,圓錐側面造價為![]()
![]() 元
元![]() .
.
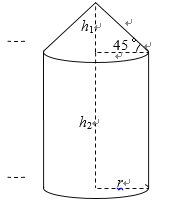
(1)將圓柱的高![]() 表示為底面半徑
表示為底面半徑![]() 的函數,并求出定義域;
的函數,并求出定義域;
(2)當容器造價最低時,圓柱的底面半徑![]() 為多少?
為多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com