
【題目】已知函數(shù)![]() .
.
(1)若![]() ,求
,求![]() 的值;
的值;
(2)已知某班共有![]() 人,記這
人,記這![]() 人生日至少有兩人相同的概率為
人生日至少有兩人相同的概率為![]() ,
,![]() ,將一年看作365天.
,將一年看作365天.
(i)求![]() 的表達式;
的表達式;
(ii)估計![]() 的近似值(精確到0.01).
的近似值(精確到0.01).
參考數(shù)值:![]() ,
,![]() ,
,![]() .
.
【答案】(1) ![]() (2) (i)
(2) (i)![]() (ii)
(ii)![]()
【解析】
(1)先討論![]() 取不同范圍內(nèi)的值時函數(shù)的定義域,并根據(jù)函數(shù)值判斷出
取不同范圍內(nèi)的值時函數(shù)的定義域,并根據(jù)函數(shù)值判斷出![]() 是
是![]() 的極小值點。通過極值點處
的極小值點。通過極值點處![]() ,求得導函數(shù)代入即可求得
,求得導函數(shù)代入即可求得![]() 的值。求出
的值。求出![]() 的值后,再代回函數(shù)
的值后,再代回函數(shù)![]() ,證明
,證明![]() 即可。
即可。
(2)每個人生日都不同的概率為![]() ,所以根據(jù)對立事件的概率即可求得至少有兩個人生日相同的概率。
,所以根據(jù)對立事件的概率即可求得至少有兩個人生日相同的概率。
將![]() 代入i中得到的式子,可得
代入i中得到的式子,可得![]() ,令
,令![]() ,左右同取對數(shù)則
,左右同取對數(shù)則![]() ,進而可得t的范圍,結合參考數(shù)據(jù)可求得
,進而可得t的范圍,結合參考數(shù)據(jù)可求得![]() 的近似值。
的近似值。
(1)由題得,當![]() 時,
時,![]() 的定義域為
的定義域為![]() ;
;
當![]() 時,
時,![]() 的定義域為
的定義域為![]() ,
,
又![]() ,且
,且![]() ,
,
所以![]() 是
是![]() 的極小值點,故
的極小值點,故![]() .
.
而![]() ,于是
,于是![]() ,解得
,解得![]() .
.
下面證明當![]() 時,
時,![]() .
.
當![]() 時,
時,![]() ,
,![]() ,
,![]() ,
,
所以當![]() 時,
時,![]() ,
,![]() 單調(diào)遞增;當
單調(diào)遞增;當![]() 時,
時,![]() ,
,![]() 單調(diào)遞減,
單調(diào)遞減,
所以![]() ,即
,即![]() 符合題意.
符合題意.
綜上,![]() .
.
(2)(i)由于![]() 人生日都不相同的概率為
人生日都不相同的概率為![]() ,
,
故![]() 人生日至少有兩人相同的概率為
人生日至少有兩人相同的概率為![]() .
.
(ii)由(1)可得當![]() 時,
時,![]() ,即
,即![]() ,當且僅當
,當且僅當![]() 時取等號,
時取等號,
由(i)得![]()
![]() .
.
記![]() ,
,
則![]()
![]()
![]() ,
,
即![]()
由參考數(shù)值得![]()
于是![]()
故![]() .
.


科目:高中數(shù)學 來源: 題型:
【題目】已知拋物線![]() :
:![]() ,直線
,直線![]() :
:![]() .
.
(1)若直線![]() 與拋物線
與拋物線![]() 相切,求直線
相切,求直線![]() 的方程;
的方程;
(2)設![]() ,直線
,直線![]() 與拋物線
與拋物線![]() 交于不同的兩點
交于不同的兩點![]() ,
,![]() ,若存在點
,若存在點![]() ,滿足
,滿足![]() ,且線段
,且線段![]() 與
與![]() 互相平分(
互相平分(![]() 為原點),求
為原點),求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某班級期末考試后,對數(shù)學成績在![]() 分以上(含
分以上(含![]() 分)的學生成績進行統(tǒng)計,其頻率分布直方圖如圖所示.其中
分)的學生成績進行統(tǒng)計,其頻率分布直方圖如圖所示.其中![]() 分數(shù)段的人數(shù)為
分數(shù)段的人數(shù)為![]() 人.
人.
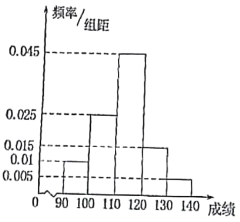
(1)根據(jù)頻率分布直方圖,寫出該班級學生數(shù)學成績的眾數(shù);
(2)現(xiàn)根據(jù)學生數(shù)學成績從第一組和第四組(從低分段到高分段依次為第一組,第二組,![]() ,第五組)中任意選出兩人形成學習小組.若選出的兩人成績之差大于
,第五組)中任意選出兩人形成學習小組.若選出的兩人成績之差大于![]() 分則稱這兩人為“最佳組合”,試求選出的兩人為“最佳組合”的概率.
分則稱這兩人為“最佳組合”,試求選出的兩人為“最佳組合”的概率.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】下列四個結論:
①在回歸分析模型中,殘差平方和越大,說明模型的擬合效果越好;
②某學校有男教師60名、女教師40名,為了解教師的體育愛好情況,在全體教師中抽取20名調(diào)查,則宜采用的抽樣方法是分層抽樣;
③線性相關系數(shù)![]() 越大,兩個變量的線性相關性越弱;反之,線性相關性越強;
越大,兩個變量的線性相關性越弱;反之,線性相關性越強;
④在回歸方程![]() 中,當解釋變量
中,當解釋變量![]() 每增加一個單位時,預報變量
每增加一個單位時,預報變量![]() 增加0.5個單位.
增加0.5個單位.
其中正確的結論是( )
A. ①②B. ①④
C. ②③D. ②④
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
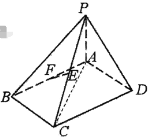
【題目】如圖,四棱錐P-ABCD中,底面ABCD為菱形,![]() 底面ABCD,
底面ABCD,![]() ,
,![]() ,E、F分別是PC和AB的中點.
,E、F分別是PC和AB的中點.
(1)證明:![]() 平面PAD;
平面PAD;
(2)若![]() ,求PD與平面PBC所成角的正弦值.
,求PD與平面PBC所成角的正弦值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知關于x的一元二次函數(shù)f(x)=ax2﹣2bx+8.
(1)設集合P={1,2,3}和Q={2,3,4,5},分別從集合P和Q中隨機取一個數(shù)作為a和b,求函數(shù)y=f(x)在區(qū)間(﹣∞,2]上有零點且為減函數(shù)的概率?
(2)設集合P=[1,3]和Q[2,5],分別從集合P和Q中隨機取一個實數(shù)作為a和b,求函數(shù)y=f(x)在區(qū)間(﹣∞,2]上有零點且為減函數(shù)的概率?
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】為推動更多人閱讀,聯(lián)合國教科文組織確定每年的4月23日為“世界讀書日”設立目的是希望居住在世界各地的人,無論你是年老還是年輕,無論你是貧窮還是富裕,都能享受閱讀的樂趣,都能尊重和感謝為人類文明做出過巨大貢獻的思想大師們,都能保護知識產(chǎn)權.為了解不同年齡段居民的主要閱讀方式,某校興趣小組在全市隨機調(diào)查了200名居民,經(jīng)統(tǒng)計這200人中通過電子閱讀與紙質(zhì)閱讀的人數(shù)之比為3:1,將這200人按年齡分組,其中統(tǒng)計通過電子閱讀的居民得到的頻率分布直方圖如圖所示,
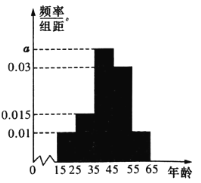
(1)求a的值及通過電子閱讀的居民的平均年鹼;
(2)把年齡在第1,2,3組的居民稱為青少年組,年齡在第4,5組的居民稱為中老年組,若選出的200人中通過紙質(zhì)閱讀的中老年有30人,請完成下面2×2列聯(lián)表,并判斷是否有97.5%的把握認為閱讀方式與年齡有關?

參考公式:![]() .
.

查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某校為了了解學生對消防知識的了解情況,從高一年級和高二年級各選取100名同學進行消防知識競賽.下圖(1)和圖(2)分別是對高一年級和高二年級參加競賽的學生成績按![]() 分組,得到的頻率分布直方圖.
分組,得到的頻率分布直方圖.
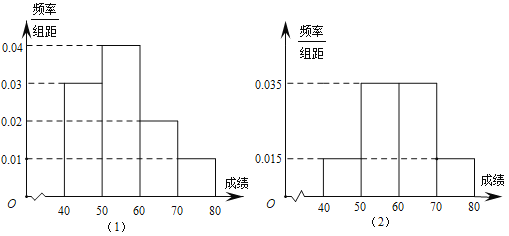
(1)請計算高一年級和高二年級成績小于60分的人數(shù);
(2)完成下面![]() 列聯(lián)表,并回答:有多大的把握可以認為“學生所在的年級與消防常識的了解存在相關性”?
列聯(lián)表,并回答:有多大的把握可以認為“學生所在的年級與消防常識的了解存在相關性”?
成績小于60分人數(shù) | 成績不小于60分人數(shù) | 合計 | |
高一 | |||
高二 | |||
合計 |
附:臨界值表及參考公式:![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com