【題目】已知平面向
，滿足
，且
，
與
夾角余弦值的最小值等于_________.
【答案】
【解析】
根據平面向量數量積的運算律化簡
,結合題中所給模長用
表示出
,即可用表示出
與
夾角
的余弦值;利用換元法令
,由平面向量數量積定義及三角函數的值域,求得
的范圍.代入
中求得m的取值范圍.再根據平面向量數量積定義,用m表示出
與夾角余弦值,即可由m的取值范圍結合表達式的性質得解.
平面向
,滿足
,則
因為
展開化簡可得
,
因為
,代入化簡可得
設與的夾角為
則由上式可得
而
代入上式化簡可得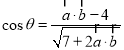
令,設
與
的夾角為
,則由平面向量數量積定義可得
,而
所以
由余弦函數的值域可得,即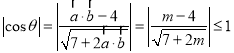
將不等式化簡可得
,解不等式可得
綜上可得
,即
而由平面向量數量積的運算可知,設與夾角為
,
則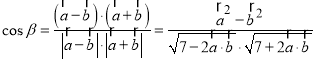
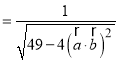
當分母越大時,
的值越小;當的值越小時,分母的值越大
所以當
時, 的值最小
代入可得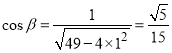
所以與夾角余弦值的最小值等于
故答案為:
科目：高中數學 來源： 題型：
【題目】2019年某地初中畢業升學體育考試規定：考生必須參加長跑、擲實心球、1分鐘跳繩三項測試，三項測試各項20分，滿分60分．某學校在初三上學期開始時，為掌握全年級學生1分鐘跳繩情況，按照男女比例利用分層抽樣抽取了100名學生進行測試，其中女生54人，得到下面的頻率分布直方圖，計分規則如表1：
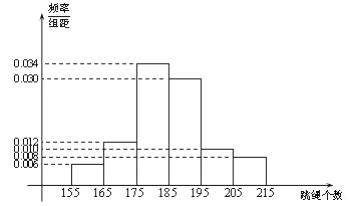
表1
每分鐘跳繩個數 |
|
|
|
|
得分 | 17 | 18 | 19 | 20 |
（1）規定：學生1分鐘跳繩得分20分為優秀，在抽取的100名學生中，男生跳繩個數大于等于185個的有28人，根據已知條件完成表2，并根據這100名學生測試成績，能否有99%的把握認為學生1分鐘跳繩成績優秀與性別有關？
表2
跳繩個數 |
|
| 合計 |
男生 | 28 | ||
女生 | 54 | ||
合計 | 100 |
附：參考公式：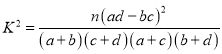
臨界值表：
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
（2）根據往年經驗，該校初三年級學生經過一年的訓練，正式測試時每人每分鐘跳繩個數都有明顯進步．假設今年正式測試時每人每分鐘跳繩個數比初三上學期開始時個數增加10個，全年級恰有2000名學生，所有學生的跳繩個數
服從正態分布
（用樣本數據的平均值和方差估計總體的期望和方差，各組數據用中點值代替）．
①估計正式測試時，1分鐘跳182個以上的人數（結果四舍五入到整數）；
②若在全年級所有學生中任意選取3人，正式測試時1分鐘跳195個以上的人數為
，求的分布列及期望．
附：若隨機變量服從正態分布，則
，
，
．
．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為了解兒子身高與其父親身高的關系，隨機調查了5對父子的身高，統計數據如下表所示．
編 號 | A | B | C | D | E |
父親身高 | 174 | 176 | 176 | 176 | 178 |
兒子身高 | 175 | 175 | 176 | 177 | 177 |
（1）從這五對父子任意選取兩對，用編號表示出所有可能取得的結果，并求隨機事件
“兩對父子中兒子的身高都不低于父親的身高”發生的概率；
（2）由表中數據，利用“最小二乘法”求
關于
的回歸直線的方程．
參考公式：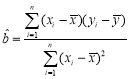
，
；回歸直線：
．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】平面直角坐標系xOy內，點
，動點
和Q關于原點O對稱，
，
.
（1）以原點O和點A為頂點作等腰直角三角形ABO，使
，求向量
坐標；
（2）若
且P、M、A三點共線，求
的最小值；
（3）若
，且
，
，求直線AQ的解析式.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知兩個不相等的非零向量
與
，兩組向量
，
，
，
，
和
，
，
，
，
均有2個和3個按照某種順序排成一列所構成，記
，且
表示
所有可能取值中的最小值，有以下結論：①有5個不同的值；②若
，則與
無關；③ 若∥，則與
無關；④ 若
，則
；⑤若
，且
，則與的夾角為
；正確的結論的序號是（ ）
A.①②④B.②④C.②③D.①⑤
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】關于下列結論：
①函數
是偶函數；
②直線
是函數
的圖象的一條對稱軸；
③將函數的圖象向左平移
個單位后，所得圖象的函數解析式為
；
④函數
的圖象關于點
成中心對稱.
其中所有正確結論的序號為______.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某單位有員工1000名，平均每人每年創造利潤10萬元．為增加企業競爭力，決定優化產業結構，調整出
名員工從事第三產業，調整后平均每人每年創造利潤為
萬元
，剩下的員工平均每人每年創造的利潤可以提高
．
（1）若要保證剩余員工創造的年總利潤不低于原來1000名員工創造的年總利潤，則最多調整出多少名員工從事第三產業？
（2）若要保證剩余員工創造的年總利潤不低于原來1000名員工創造的年總利潤條件下，若要求調整出的員工創造出的年總利潤始終不高于剩余員工創造的年總利潤，則
的取值范圍是多少？
查看答案和解析>>
科目：高中數學 來源： 題型：
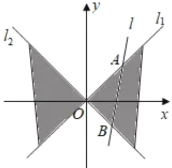
【題目】如圖，在平面直角坐標系
中，直線
與直線
之間的陰影部分記為
，區域中動點
到
的距離之積為1.
（1）求點
的軌跡
的方程；
（2）對于區域中動點
，求
的取值范圍；
（3）動直線
穿過區域，分別交直線于
兩點，若直線與點的軌跡有且只有一個公共點，求證：
的面積值為定值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
