
【題目】已知集合P={x|x2-8x-20≤0},S={x||x-1|≤m}.
(1)若(P∪S)P,求實數m的取值范圍;
(2)是否存在實數m,使得“x∈P”是“x∈S”的充要條件?若存在,求出m的取值范圍;若不存在,請說明理由.
科目:高中數學 來源: 題型:
【題目】某工廠有120名工人,其年齡都在20~ 60歲之間,各年齡段人數按[20,30),[30,40),[40,50),[50,60]分成四組,其頻率分布直方圖如下圖所示.工廠為了開發新產品,引進了新的生產設備。現采用分層抽樣法從全廠工人中抽取一個容量為20的樣本參加新設備培訓,培訓結束后進行結業考試。已知各年齡段培訓結業考試成績優秀的人數如下表所示:

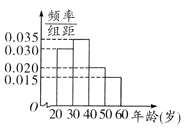
若隨機從年齡段[20,30)和[40,50)的參加培訓工人中各抽取1人,則這兩人培訓結業考試成績恰有一人優秀的概率為___________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知圓![]() 的方程為
的方程為![]() ,圓
,圓![]() 的方程為
的方程為![]() ,若動圓
,若動圓![]() 與圓
與圓![]() 內切,與圓
內切,與圓![]() 外切.
外切.

(1)求動圓圓心![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)過直線![]() 上的點
上的點![]() 作圓
作圓![]() 的兩條切線,設切點分別是
的兩條切線,設切點分別是![]() ,
,![]() ,若直線
,若直線![]() 與軌跡
與軌跡![]() 交于
交于![]() ,
,![]() 兩點,求
兩點,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某研究所計劃利用宇宙飛船進行新產品搭載試驗,計劃搭載若干件新產品A,B,該研究所要根據產品的研制成本、產品重量、搭載試驗費用和預計收益來決定具體安排,通過調查得到的有關數據如表:
每件A產品 | 每件B產品 | |
研制成本、搭載試驗 費用之和(萬元) | 20 | 30 |
產品重量(千克) | 10 | 5 |
預計收益(萬元) | 80 | 60 |
已知研制成本、搭載試驗費用之和的最大資金為300萬元,最大搭載重量為110千克,則如何安排這兩種產品進行搭載,才能使總預計收益達到最大,求最大預計收益是多少.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校要定制高一年級的校服,學生根據廠家提供的參考身高選擇校服規格.據統計,高一年級女生需要不同規格校服的頻數如表所示.
校服規格 | 155 | 160 | 165 | 170 | 175 | 合計 |
頻數 | 39 | 64 | 167 | 90 | 26 | 386 |
如果用一個量來代表該校高一年級女生所需校服的規格,那么在中位數、平均數和眾數中,哪個量比較合適?試討論用表中的數據估計全國高一年級女生校服規格的合理性.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】將一顆質地均勻的骰子(它是一種各面上分別標有點數1、2、3、4、5、6的正方體玩具)先后拋擲2次,記第一次出現的點數為m,記第二次出現的點數為n,向量![]() 則
則![]() 和
和![]() 共線的概率為
共線的概率為
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國是世界嚴重缺水的國家,城市缺水問題較為突出,某市政府為了鼓勵居民節約用水,計劃在本市試行居民生活用水定額管理,即確定一個合理的居民月用水量標準![]() (噸),用水量不超過
(噸),用水量不超過![]() 的部分按平價收費,超過
的部分按平價收費,超過![]() 的部分按議價收費,為了了解全市民月用水量的分布情況,通過抽樣,獲得了100位居民某年的月用水量(單位:噸),將數據按照
的部分按議價收費,為了了解全市民月用水量的分布情況,通過抽樣,獲得了100位居民某年的月用水量(單位:噸),將數據按照![]() 分成9組,制成了如圖所示的頻率分布直方圖.
分成9組,制成了如圖所示的頻率分布直方圖.

(Ⅰ)求直方圖中的![]() 值;
值;
(Ⅱ)已知平價收費標準為![]() 元/噸,議價收費標準為
元/噸,議價收費標準為![]() 元/噸,當
元/噸,當![]() 時,估計該市居民的月平均水費.(同一組中的數據用該組區間的中點值代替)
時,估計該市居民的月平均水費.(同一組中的數據用該組區間的中點值代替)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國是世界嚴重缺水的國家,城市缺水問題較為突出,某市政府為了鼓勵居民節約用水,計劃在本市試行居民生活用水定額管理,即確定一個合理的居民月用水量標準![]() (噸),用水量不超過
(噸),用水量不超過![]() 的部分按平價收費,超過
的部分按平價收費,超過![]() 的部分按議價收費,為了了解全市民月用水量的分布情況,通過抽樣,獲得了100位居民某年的月用水量(單位:噸),將數據按照
的部分按議價收費,為了了解全市民月用水量的分布情況,通過抽樣,獲得了100位居民某年的月用水量(單位:噸),將數據按照![]() 分成9組,制成了如圖所示的頻率分布直方圖.
分成9組,制成了如圖所示的頻率分布直方圖.

(Ⅰ)若全市居民中月均用水量不低于3噸的人數為3.6萬,試估計全市有多少居民?并說明理由;
(Ⅱ)若該市政府擬采取分層抽樣的方法在用水量噸數為![]() 和
和![]() 之間選取7戶居民作為議價水費價格聽證會的代表,并決定會后從這7戶家庭中按抽簽方式選出4戶頒發“低碳環保家庭”獎,設
之間選取7戶居民作為議價水費價格聽證會的代表,并決定會后從這7戶家庭中按抽簽方式選出4戶頒發“低碳環保家庭”獎,設![]() 為用水量噸數在
為用水量噸數在![]() 中的獲獎的家庭數,
中的獲獎的家庭數,![]() 為用水量噸數在
為用水量噸數在![]() 中的獲獎家庭數,記隨機變量
中的獲獎家庭數,記隨機變量![]() ,求
,求![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com