
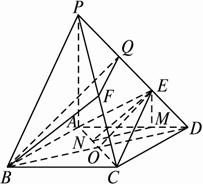
(1)求二面角EACD的?大小?.
(2)在棱PC上是否存在一點F,使BF∥平面AEC?若存在,求出點F;若不存在,請說明理由.
解析:(1)作EM⊥AD于M,?
 ?
?
∵PA⊥平面ABCD,?
∴平面PAD⊥平面ABCD.?
∴EM⊥平面ABCD.?
作MN⊥AC于N,連結(jié)NE,則NE⊥AC.∴∠ENM即為二面角E-AC-D的平面角.?
∵EM=![]() PA=
PA=![]() a,AM =
a,AM =![]() a?,?
a?,?
∴MN=AM·sin60°=![]() a·
a·![]() =
=![]() a.??
a.??
∴tan∠ENM=![]() .
.
∴∠ENM=30°.?
∴二面角EACD的大小為30°.?
(2)法一 :取PC中點F,PE中點Q,連結(jié)FQ、BF、BQ,設(shè)AC∩BD=O,連OE,?
則OE∥BQ,QF∥CE,∴平面BQF∥平面ACE.?
∴BF∥平面ACE.?
∴在棱PC上存在中點F,使BF∥平面AEC.?
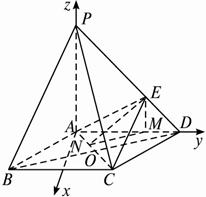
法二:建系,A(0,0,0)如圖,B(![]() a ,
a ,![]() a ,0),D(0,a,0),C(
a ,0),D(0,a,0),C(![]() a ,
a ,![]() a,0),P(0,0,a),E(0,
a,0),P(0,0,a),E(0,![]() a ,
a ,![]() a),
a),
∴![]() =(0,
=(0,![]() a,
a,![]() a),
a),![]() =(
=(![]() a,
a,![]() a,0),
a,0),![]() =(
=(![]() a,
a,![]() a,-a).?
a,-a).?
設(shè)![]() =λ
=λ![]() =(
=(![]() λa,
λa,![]() λa,-λa),又
λa,-λa),又![]() =(-
=(-![]() a,
a,![]() a,a),?
a,a),?
∴![]() =
=![]() +
+![]() =(
=(![]() a(λ-1),
a(λ-1),![]() (1+λ)a ,a(1-λ)).?
(1+λ)a ,a(1-λ)).?
令![]() =λ1
=λ1![]() +λ2
+λ2![]() ,?
,?
∴![]() =λ1(
=λ1(![]() a,
a, ![]() a,0)+λ2(0,
a,0)+λ2(0,![]() a,
a,![]() a),?
a),?

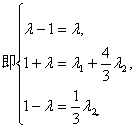 ?
?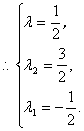
∴當(dāng)λ=![]() 時,
時,![]() =-
=-![]()
![]() +
+![]()
![]() ,即
,即![]() 與
與![]() 、
、![]() 共面,此時F為BC中點.?
共面,此時F為BC中點.?
又BF![]() 平面ACE,∴BF∥平面ACE.?
平面ACE,∴BF∥平面ACE.?
法三:取PC中點F,由![]()
??
![]()
![]() ?
?
![]()
=![]() ,?
,?
∴![]() 與
與![]() 、
、![]() 共面.又BF
共面.又BF![]() 平面ACE,∴BF∥平面ACE.
平面ACE,∴BF∥平面ACE.


科目:高中數(shù)學(xué) 來源: 題型:
 如圖,在底面是菱形的四棱錐P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=
如圖,在底面是菱形的四棱錐P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=| 2 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
 如圖,在底面是菱形的四棱錐P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=
如圖,在底面是菱形的四棱錐P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=| 2 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
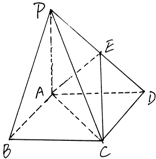 在底面是菱形的四棱錐P-ABCD中,PA⊥底面ABCD,∠ABC=60°,PA=AB=2,E是PD中點.
在底面是菱形的四棱錐P-ABCD中,PA⊥底面ABCD,∠ABC=60°,PA=AB=2,E是PD中點.查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
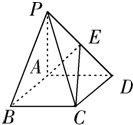 如圖,在底面是菱形的四棱錐P-ABCD,∠ABC=60°,PA=AC=a,PB=PD=
如圖,在底面是菱形的四棱錐P-ABCD,∠ABC=60°,PA=AC=a,PB=PD=| 2 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
 如圖,在底面是菱形的四棱錐 P-ABCD中,∠ABC=60°,PA⊥平面ABCD,點E、F、G分別為CD、PD、PB的中點.PA=AD=2.
如圖,在底面是菱形的四棱錐 P-ABCD中,∠ABC=60°,PA⊥平面ABCD,點E、F、G分別為CD、PD、PB的中點.PA=AD=2.查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com