
【題目】設(shè)函數(shù)f(x)=3x2﹣4ax(a>0)與g(x)=2a2lnx+b有公共點(diǎn),且在公共點(diǎn)處的切線方程相同,則實(shí)數(shù)b的最大值為( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】A
【解析】解:設(shè)y=f(x)與y=g(x)(x>0)在公共點(diǎn)P(x0,y0)處的切線相同、
f′(x)=6x﹣4a,g′(x)= ![]() ,
,
由題意f(x0)=g(x0),f′(x0)=g′(x0),
即3x02﹣4ax0=2a2lnx0+b,6x0﹣4a= ![]()
由3x0﹣2a= ![]() 得x0=a或x0=﹣
得x0=a或x0=﹣ ![]() a(舍去),
a(舍去),
即有b=﹣a2﹣2a2lna.
令h(t)=﹣t2﹣2t2lnt(t>0),則h′(t)=﹣4t(1+lnt),
于是當(dāng)﹣4t(1+lnt)>0,即0<t< ![]() 時(shí),h′(t)>0;
時(shí),h′(t)>0;
當(dāng)﹣4t(1+lnt)<0,即t> ![]() 時(shí),h′(t)<0.
時(shí),h′(t)<0.
故h(t)在(0, ![]() )為增函數(shù),在(
)為增函數(shù),在( ![]() ,+∞)為減函數(shù),
,+∞)為減函數(shù),
于是h(t)在(0,+∞)的最大值為h( ![]() )=
)= ![]() ,
,
故b的最大值為 ![]() .
.
所以答案是:A.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】我國(guó)南宋數(shù)學(xué)家秦九韶所著《數(shù)學(xué)九章》中有“米谷粒分”問(wèn)題:糧倉(cāng)開倉(cāng)收糧,糧農(nóng)送來(lái)米1512石,驗(yàn)得米內(nèi)夾谷,抽樣取米一把,數(shù)得216粒內(nèi)夾谷27粒,則這批米內(nèi)夾谷約( )
A.164石
B.178石
C.189石
D.196石
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)f(x)滿足f(x+1)=﹣f(x﹣1),且當(dāng)x∈(0,2)時(shí),f(x)=2x , 則f(log280)= .
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】下列四個(gè)命題中正確是( )
A.函數(shù)y=ax(a>0且a≠1)與函數(shù) ![]() (a>0且a≠1)的值域相同
(a>0且a≠1)的值域相同
B.函數(shù)y=![]() 與y=
與y=![]() 的值域相同
的值域相同
C.函數(shù) ![]() 與
與 ![]() 都是奇函數(shù)
都是奇函數(shù)
D.函數(shù)y=![]() 與y=2x﹣1在區(qū)間[0,+∞)上都是增函數(shù).
與y=2x﹣1在區(qū)間[0,+∞)上都是增函數(shù).
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù) ![]()
(1)判斷函數(shù)f(x)的奇偶性,并說(shuō)明理由;
(2)證明:f(x)在(﹣1,+∞)上為增函數(shù);
(3)證明:方程f(x)=0沒(méi)有負(fù)數(shù)根.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】設(shè)函數(shù)f(x)=Asin(ωx+φ)(其中A,ω,φ為常數(shù)且A>0,ω>0, ![]() )的部分圖象如圖所示,若
)的部分圖象如圖所示,若 ![]() (
( ![]() ),則
),則 ![]() 的值為 .
的值為 . 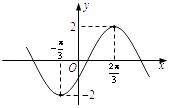
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】設(shè)△ABC的三個(gè)內(nèi)角分別為A,B,C.向量 ![]() 共線. (Ⅰ)求角C的大小;
共線. (Ⅰ)求角C的大小;
(Ⅱ)設(shè)角A,B,C的對(duì)邊分別是a,b,c,且滿足2acosC+c=2b,試判斷△ABC的形狀.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在四棱錐 ![]() 中,底面
中,底面 ![]() 是菱形,
是菱形, ![]() ,
, ![]() 平面
平面 ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 是
是 ![]() 中點(diǎn).
中點(diǎn).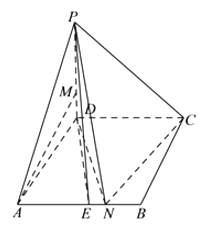
(I)求證:直線 ![]() 平面
平面 ![]() .
.
(II)求證:直線 ![]() 平面
平面 ![]() .
.
(III)在 ![]() 上是否存在一點(diǎn)
上是否存在一點(diǎn) ![]() ,使得二面角
,使得二面角 ![]() 的大小為
的大小為 ![]() ,若存在,確定
,若存在,確定 ![]() 的位置,若不存在,說(shuō)明理由.
的位置,若不存在,說(shuō)明理由.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com