
(本小題滿分18分)設數列{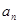 }的前
}的前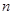 項和為
項和為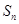 ,且滿足
,且滿足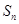 =2-
=2-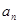 ,(
,(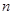 =1,2,3,…)
=1,2,3,…)
(Ⅰ)求數列{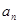 }的通項公式;
}的通項公式;
(Ⅱ)若數列{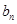 }滿足
}滿足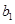 =1,且
=1,且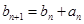 ,求數列{
,求數列{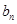 }的通項公式;
}的通項公式;
(Ⅲ)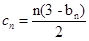 ,求
,求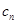 的前
的前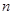 項和
項和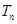
(Ⅰ) an=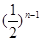 (n∈N*); (Ⅱ) bn=3-2(
(n∈N*); (Ⅱ) bn=3-2(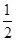 )n-; (Ⅲ)
)n-; (Ⅲ) 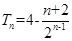 。
。
解析試題分析:(Ⅰ)∵n=1時,a1+S1=a1+a1=2
∴a1=1
∵Sn=2-an即an+Sn=2 ∴an+1+Sn+1=2
兩式相減:an+1-an+Sn+1-Sn=0
即an+1-an+an+1=0,故有2an+1=an
∵an≠0 ∴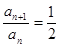 (n∈N*)
(n∈N*)
所以,數列{an}為首項a1=1,公比為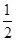 的等比數列.an=
的等比數列.an=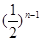 (n∈N*)
(n∈N*)
(Ⅱ)∵bn+1=bn+an(n=1,2,3,…)
∴bn+1-bn=(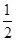 )n-1
)n-1
得b2-b1=1
b3-b2=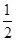
b4-b3=(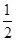 )2
)2
……
bn-bn-1=(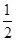 )n-2(n=2,3,…)
)n-2(n=2,3,…)
將這n-1個等式相加,得
bn-b1=1+
又∵b1=1,∴bn=3-2(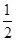 )n-1(n=1,2,3,…)
)n-1(n=1,2,3,…)
(3)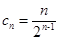
所以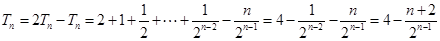
考點:數列通項公式的求法;數列前n項和的求法。
點評:若已知遞推公式為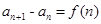 的形式求通項公式常用累加法。
的形式求通項公式常用累加法。
注:①若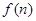 是關于n的一次函數,累加后可轉化為等差數列求和;
是關于n的一次函數,累加后可轉化為等差數列求和;
②若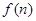 是關于n的二次函數,累加后可分組求和;
是關于n的二次函數,累加后可分組求和;
③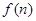 是關于n的指數函數,累加后可轉化為等比數列求和;
是關于n的指數函數,累加后可轉化為等比數列求和;
④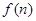 是關于n的分式函數,累加后可裂項求和。
是關于n的分式函數,累加后可裂項求和。


 名師點睛字詞句段篇系列答案
名師點睛字詞句段篇系列答案科目:高中數學 來源: 題型:解答題
(本小題滿分14分)
已知點(1,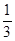 )是函數
)是函數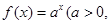 且
且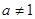 )的圖象上一點,等比數列
)的圖象上一點,等比數列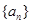 的前
的前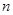 項和為
項和為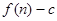 ,數列
,數列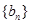
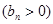 的首項為
的首項為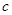 ,且前
,且前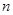 項和
項和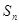 滿足
滿足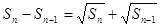 (
(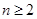 ).
).
(1)求數列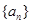 和
和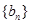 的通項公式;
的通項公式;
(2)若數列{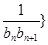 前
前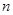 項和為
項和為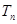 ,問
,問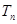 >
>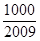 的最小正整數
的最小正整數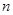 是多少?
是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分12分)a2,a5是方程x 2-12x+27=0的兩根,數列{ }是公差為正數的等差數列,數列{
}是公差為正數的等差數列,數列{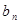 }的前n項和為
}的前n項和為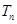 ,且
,且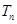 =1-
=1-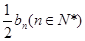
(1)求數列{ },{
},{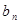 }的通項公式;
}的通項公式;
(2)記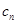 =
=
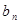 ,求數列{
,求數列{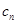 }的前n項和Sn.
}的前n項和Sn.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
定義數列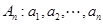 ,(例如
,(例如 時,
時,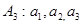 )滿足
)滿足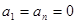 ,且當
,且當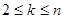 (
(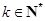 )時,
)時,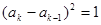 .令
.令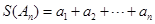 .
.
(1)寫出數列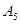 的所有可能的情況;(5分)
的所有可能的情況;(5分)
(2)設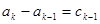 ,求
,求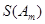 (用
(用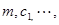
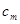 的代數式來表示);(5分)
的代數式來表示);(5分)
(3)求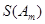 的最大值.(6分)
的最大值.(6分)
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本題滿分12分)已知函數 數列
數列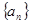 的前n項和為
的前n項和為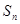 ,
, ,在曲線
,在曲線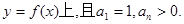
(1)求數列{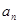 }的通項公式
}的通項公式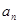 ;(II)數列{
;(II)數列{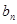 }首項b1=1,前n項和Tn,且
}首項b1=1,前n項和Tn,且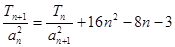 ,求數列{
,求數列{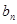 }通項公式bn.
}通項公式bn.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com