Question

【題目】在正方體ABCD-A1B1C1D1中，M、N分別為棱BC和棱CC1的中點，則異面直線AC和MN所成的角為（ ）

A. 30° B. 45° C. 90° D. 60°

Answer 1

【答案】D

【解析】

以D為原點，DA，DC，DD1 分別為x，y，z軸，建立空間直角坐標(biāo)系，利用向量法能求出異面直線AC和MN所成的角．

以D為原點，DA，DC，DD1 分別為x，y，z軸，建立空間直角坐標(biāo)系，

設(shè)正方體ABCD﹣A1B1C1D1中棱長為2，

∵M(jìn)、N分別為棱BC和棱CC1的中點，

∴M（1，2，0），N（0，2，1），A（2，0，0），C（0，2，0），

＝（﹣1，0，1），＝（﹣2，2，0），

設(shè)異面直線AC和MN所成的角為θ，

則cosθ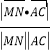＝＝＝ ， 0<θ< ∴θ＝60°．

∴異面直線AC和MN所成的角為60°．

故選：D．