
(本小題滿分14分)已知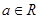 且
且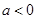 ,設(shè)函數(shù)
,設(shè)函數(shù)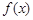 = ax2 +x-3alnx.
= ax2 +x-3alnx.
(I)求函數(shù) 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(II)當(dāng)a=-1時(shí),證明: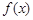 ≤2x-2.
≤2x-2.
(I) 的單調(diào)遞增區(qū)間為(0,
的單調(diào)遞增區(qū)間為(0,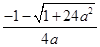 )、遞減區(qū)間為(
)、遞減區(qū)間為(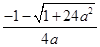 ,
,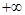 ); (II)見解析。
); (II)見解析。
解析試題分析:(I)先求出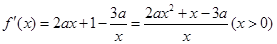 ,然后再根據(jù)導(dǎo)數(shù)大于(小于)零,分別求出其單調(diào)增(減)區(qū)間.
,然后再根據(jù)導(dǎo)數(shù)大于(小于)零,分別求出其單調(diào)增(減)區(qū)間.
(II)當(dāng)a=-1時(shí),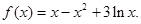 ,然后構(gòu)造函數(shù)
,然后構(gòu)造函數(shù)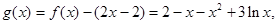 再利用導(dǎo)數(shù)求g(x)的最大值,證明其最大值不大于零即可.
再利用導(dǎo)數(shù)求g(x)的最大值,證明其最大值不大于零即可.
(I) 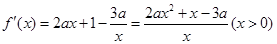 …………………………1分
…………………………1分
令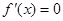 解得
解得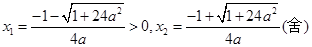 …………………3分
…………………3分
列表如下:
…………………6分x (0, 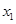 )
) ( 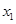 ,
,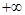 )
)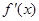
+ - 


故 的單調(diào)遞增區(qū)間為(0,
的單調(diào)遞增區(qū)間為(0,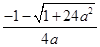 )、遞減區(qū)間為(
)、遞減區(qū)間為(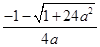 ,
,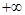 )…………………7分
)…………………7分
(II)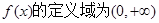 ,a=-1時(shí),
,a=-1時(shí),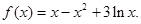
設(shè)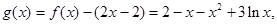 ………………………………9分
………………………………9分
則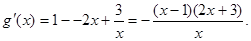 ……………………10分
……………………10分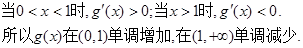 ……………………12分
……………………12分
而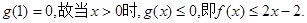 ……………………14分
……………………14分
考點(diǎn):導(dǎo)數(shù)在研究函數(shù)的單調(diào)性,極值,最值,證明不等式中的應(yīng)用.
點(diǎn)評(píng):利用導(dǎo)數(shù)求單調(diào)區(qū)間時(shí):如果含有參數(shù),要注意分類討論,并且要注意函數(shù)的定義域.
證明不等式的問題可以通過構(gòu)造函數(shù),通過導(dǎo)數(shù)研究函數(shù)的最值證明不等式是常用的策略之一.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本題滿分16分)某公司將進(jìn)貨單價(jià)為8元一個(gè)的商品按10元一個(gè)銷售,每天可賣出100個(gè),若這種商品的銷售價(jià)每個(gè)上漲1元,則銷售量就減少10個(gè).
(1)求函數(shù)解析式;
(1)求銷售價(jià)為13元時(shí)每天的銷售利潤;
(2)如果銷售利潤為360元,那么銷售價(jià)上漲了幾元?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本小題滿分14分)
已知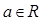 ,函數(shù)
,函數(shù)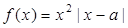 .
.
(Ⅰ)當(dāng)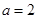 時(shí),求使
時(shí),求使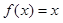 成立的
成立的 的集合;
的集合;
(Ⅱ)求函數(shù)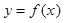 在區(qū)間
在區(qū)間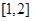 上的最小值.
上的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本小題滿分12分)設(shè)某物體一天中的溫度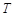 是時(shí)間
是時(shí)間 的函數(shù):
的函數(shù):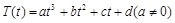 ,其中溫度的單位是
,其中溫度的單位是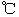 ,時(shí)間單位是小時(shí),
,時(shí)間單位是小時(shí),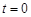 表示12:00,
表示12:00, 取正值表示12:00以后.若測得該物體在8:00的溫度是
取正值表示12:00以后.若測得該物體在8:00的溫度是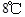 ,12:00的溫度為
,12:00的溫度為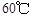 ,13:00的溫度為
,13:00的溫度為 ,且已知該物體的溫度在8:00和16:00有相同的變化率.
,且已知該物體的溫度在8:00和16:00有相同的變化率.
(1)寫出該物體的溫度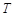 關(guān)于時(shí)間
關(guān)于時(shí)間 的函數(shù)關(guān)系式;
的函數(shù)關(guān)系式;
(2)該物體在10:00到14:00這段時(shí)間中(包括10:00和14:00),何時(shí)溫度最高,并求出最高溫度;
(3)如果規(guī)定一個(gè)函數(shù)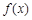 在區(qū)間
在區(qū)間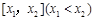 上的平均值為
上的平均值為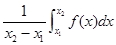 ,求該物體在8:00到16:00這段時(shí)間內(nèi)的平均溫度.
,求該物體在8:00到16:00這段時(shí)間內(nèi)的平均溫度.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
在△ABC中,內(nèi)角A,B,C所對(duì)邊長分別為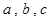 ,
,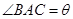 ,
,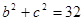 ,
, 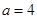 .
.
(1)求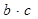 的最大值及
的最大值及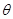 的取值范圍;
的取值范圍;
(2)求函數(shù)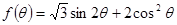 的最值. (本題滿分12分)
的最值. (本題滿分12分)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本小題12分)某產(chǎn)品原來的成本為1000元/件,售價(jià)為1200元/件,年銷售量為1萬件。由于市場飽和顧客要求提高,公司計(jì)劃投入資金進(jìn)行產(chǎn)品升級(jí)。據(jù)市場調(diào)查,若投入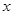 萬元,每件產(chǎn)品的成本將降低
萬元,每件產(chǎn)品的成本將降低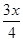 元,在售價(jià)不變的情況下,年銷售量將減少
元,在售價(jià)不變的情況下,年銷售量將減少 萬件,按上述方式進(jìn)行產(chǎn)品升級(jí)和銷售,扣除產(chǎn)品升級(jí)資金后的純利潤記為
萬件,按上述方式進(jìn)行產(chǎn)品升級(jí)和銷售,扣除產(chǎn)品升級(jí)資金后的純利潤記為 (單位:萬元).(純利潤=每件的利潤×年銷售量-投入的成本)
(單位:萬元).(純利潤=每件的利潤×年銷售量-投入的成本)
(Ⅰ)求 的函數(shù)解析式;
的函數(shù)解析式;
(Ⅱ)求 的最大值,以及
的最大值,以及 取得最大值時(shí)
取得最大值時(shí)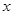 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本小題13分)已知函數(shù)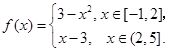
(1)在右圖給定的直角坐標(biāo)系內(nèi)畫出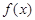 的圖象;
的圖象;
(2)寫出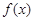 的單調(diào)遞增區(qū)間.
的單調(diào)遞增區(qū)間.
(3) 求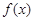 的最小值。
的最小值。
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com