
【題目】已知數列![]() ,其前
,其前![]() 項和為
項和為![]() ,滿足
,滿足![]() ,
,![]() ,其中
,其中![]() ,
,![]() ,
,![]() ,
,![]() .
.
⑴若![]() ,
,![]() ,
,![]() (
(![]() ),求證:數列
),求證:數列![]() 是等比數列;
是等比數列;
⑵若數列![]() 是等比數列,求
是等比數列,求![]() ,
,![]() 的值;
的值;
⑶若![]() ,且
,且![]() ,求證:數列
,求證:數列![]() 是等差數列.
是等差數列.
【答案】(1)見解析(2)![]() (3)見解析
(3)見解析
【解析】試題分析:(1)![]() (
(![]() ), 所以
), 所以![]() ,故數列
,故數列![]() 是等比數列;(2)利用特殊值法,得
是等比數列;(2)利用特殊值法,得![]() ,故
,故![]() ;(3)得
;(3)得![]() ,所以
,所以![]() ,得
,得![]() ,可證數列
,可證數列![]() 是等差數列.
是等差數列.
試題解析:
(1)證明:若![]() ,則當
,則當![]() (
(![]() ),
),
所以![]() ,
,
即![]() ,
,
所以![]() ,
,
又由![]() ,
,![]() ,
,
得![]() ,
,![]() ,即
,即![]() ,
,
所以![]() ,
,
故數列![]() 是等比數列.
是等比數列.
(2)若![]() 是等比數列,設其公比為
是等比數列,設其公比為![]() (
(![]() ),
),
當![]() 時,
時,![]() ,即
,即![]() ,得
,得
![]() , ①
, ①
當![]() 時,
時,![]() ,即
,即![]() ,得
,得
![]() , ②
, ②
當![]() 時,
時,![]() ,即
,即![]() ,得
,得
![]() , ③
, ③
②①![]() ,得
,得![]() ,
,
③②![]() ,得
,得![]() ,
,
解得![]() .
.
代入①式,得![]() .
.
此時![]() (
(![]() ),
),
所以![]() ,
,![]() 是公比為1的等比數列,
是公比為1的等比數列,
故![]() .
.
(3)證明:若![]() ,由
,由![]() ,得
,得![]() ,
,
又![]() ,解得
,解得![]() .
.
由![]() ,
,![]() ,
, ![]() ,
,![]() ,代入
,代入![]() 得
得![]() ,
,
所以![]() ,
,![]() ,
,![]() 成等差數列,
成等差數列,
由![]() ,得
,得![]() ,
,
兩式相減得:![]()
即![]()
所以![]()
相減得:![]()
所以![]()
所以![]()
![]() ,
,
因為![]() ,所以
,所以![]() ,
,
即數列![]() 是等差數列.
是等差數列.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】在xOy中,曲線![]() 的參數方程為
的參數方程為![]() (t為參數).在以坐標原點O為極點,x軸正半軸為極軸的極坐標系中,曲線
(t為參數).在以坐標原點O為極點,x軸正半軸為極軸的極坐標系中,曲線![]() :
:![]() ,曲線
,曲線![]() :
:![]()
![]() ,
,![]() .
.
(1)把![]() 的參數方程化為極坐標方程;
的參數方程化為極坐標方程;
(2)設![]() 分別交
分別交![]() ,
,![]() 于點P,Q,求
于點P,Q,求![]() 的面積.
的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】世界互聯網大會是由中國倡導并每年在浙江省嘉興市桐鄉烏鎮舉辦的世界性互聯網盛會,大會旨在搭建中國與世界互聯互通的國際平臺和國際互聯網共享共治的中國平臺,讓各國在爭議中求共識在共識中謀合作在合作中創共贏.2019年10月20日至22日,第六屆世界互聯網大會如期舉行,為了大會順利召開,組委會特招募了1 000名志愿者.某部門為了了解志愿者的基本情況,調查了其中100名志愿者的年齡,得到了他們年齡的中位數為34歲,年齡在![]() 歲內的人數為15,并根據調查結果畫出如圖所示的頻率分布直方圖:
歲內的人數為15,并根據調查結果畫出如圖所示的頻率分布直方圖:

(1)求![]() ,
,![]() 的值并估算出志愿者的平均年齡(同一組的數據用該組區間的中點值代表);
的值并估算出志愿者的平均年齡(同一組的數據用該組區間的中點值代表);
(2)這次大會志愿者主要通過現場報名和登錄大會官網報名,即現場和網絡兩種方式報名調查.這100位志愿者的報名方式部分數據如下表所示,完善下面的表格,通過計算說明能
否在犯錯誤的概率不超過0.001的前提下,認為“選擇哪種報名方式與性別有關系”?
男性 | 女性 | 總計 | |
現場報名 | 50 | ||
網絡報名 | 31 | ||
總計 | 50 |
參考公式及數據: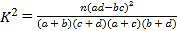 ,其中
,其中![]() .
.
| 0.05 | 0.01 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】銀川市房管局為了了解該市市民2018年1月至2019年1月期間購買二手房情況,首先隨機抽樣其中200名購房者,并對其購房面積m(單位:平方米,![]() )進行了一次調查統計,制成了如圖所示的頻率分布直方圖.
)進行了一次調查統計,制成了如圖所示的頻率分布直方圖.
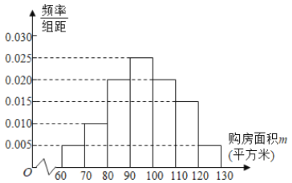
(Ⅰ)試估計該市市民的平均購房面積:
(Ⅱ)現采用分層抽樣的方法從購房面積位于![]() 的40位市民中隨機取4人,再從這4人中隨機抽取2人,求這2人的購房面積恰好有一人在
的40位市民中隨機取4人,再從這4人中隨機抽取2人,求這2人的購房面積恰好有一人在![]() 的概率,
的概率,
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)![]() ,g(x)
,g(x)![]() 1.
1.
(1)若f(a)=2,求實數a的值;
(2)判斷f(x)的單調性,并證明;
(3)設函數h(x)=g(x)![]() (x>0),若h(2t)+mh(t)+4>0對任意的正實數t恒成立,求實數m的取值范圍.
(x>0),若h(2t)+mh(t)+4>0對任意的正實數t恒成立,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)若函數![]() 在
在![]() 內為增函數,求實數
內為增函數,求實數![]() 的取值范圍;
的取值范圍;
(2)若函數![]() 在
在![]() 內恰有兩個零點,求實數
內恰有兩個零點,求實數![]() 的取值范圍;
的取值范圍;
(3)已知![]() ,試估算
,試估算![]() 的近似值,(結果精確到0.001)
的近似值,(結果精確到0.001)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com