
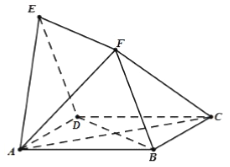
【題目】如圖,四邊形![]() 與
與![]() 均為菱形,
均為菱形,![]() ,且
,且![]() .
.
(1)求證:![]() 平面
平面![]() ;
;
(2)求證:![]() 平面
平面![]() ;
;
(3)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)證明見解析;(2)證明見解析;(3)![]() .
.
【解析】
試題分析:(1)由線面垂直的判定定理得到結論;(2)通過證明線線平行,得到線面平行;(3)建立空間直角坐標系![]() ,求出平面
,求出平面![]() 的法向量,易知
的法向量,易知![]() 面
面![]() ,所以面
,所以面![]() 的法向量為
的法向量為![]() ,再求出它們的夾角的余弦值.
,再求出它們的夾角的余弦值.
試題解析:(1)證明:設![]() 與
與![]() 相交于點
相交于點![]() ,連接
,連接![]() ,因為四邊形
,因為四邊形![]() 為菱形,所以
為菱形,所以![]() ,且
,且![]() 為
為![]() 中點,又
中點,又![]() ,所以
,所以![]() ,
,
因為![]() ,所以
,所以![]() 平面
平面![]() .
.
(2)證明:因為四邊形![]() 與
與![]() 均為菱形,
均為菱形,
所以![]() ,
,![]() ,所以平面
,所以平面![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
(3)解:因為四邊形![]() 為菱形,且
為菱形,且![]() ,所以△
,所以△![]() 為等邊三角形,
為等邊三角形,
因為![]() 為
為![]() 中點,所以
中點,所以![]() ,故
,故![]() 平面
平面![]() .
.
由![]() ,
,![]() ,
,![]() 兩兩垂直,建立如圖所示的空間直角坐標系
兩兩垂直,建立如圖所示的空間直角坐標系![]() .
.
設![]() ,因為四邊形
,因為四邊形![]() 為菱形,
為菱形,![]() ,則
,則![]() ,所以
,所以![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
所以![]() ,
,![]() .
.
設平面![]() 的法向量
的法向量![]() ,則有
,則有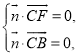 所以
所以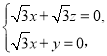
取![]() ,得
,得![]() .
.
易知平面![]() 的法向量為
的法向量為![]() .
.
由二面角![]() 是銳角,得
是銳角,得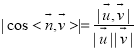
![]() ,
,
所以二面角![]() 的余弦值為
的余弦值為![]() .
.



 永乾教育寒假作業快樂假期延邊人民出版社系列答案
永乾教育寒假作業快樂假期延邊人民出版社系列答案科目:高中數學 來源: 題型:
【題目】用數字0、2、3、4、6按下列要求組數、計算:
(1)能組成多少個沒有重復數字的三位數?
(2)可以組成多少個可以被3整除的沒有重復數字的三位數?
(3)求![]() 即144的所有正約數的和.
即144的所有正約數的和.
(注:每小題結果都寫成數據形式)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠修建一個長方體無蓋蓄水池,其容積為6400立方米,深度為4米.池底每平方米的造價為120元,池壁每平方米的造價為100元.設池底長方形的長為x米.
(Ⅰ)求底面積,并用含x的表達式表示池壁面積;
(Ⅱ)怎樣設計水池能使總造價最低?最低造價是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】三國魏人劉徽,自撰《海島算經》,專論測高望遠。其中有一題:今有望海島,立兩表齊,高三丈,前后相去千步,令后表與前表相直。從前表卻行一百二十三步,人目著地取望島峰,與表末參合。從后表卻行百二十七步,人目著地取望島峰,亦與表末參合。問島高及去表各幾何? 譯文如下:要測量海島上一座山峰![]() 的高度
的高度![]() ,立兩根高均為
,立兩根高均為![]() 丈的標桿
丈的標桿![]() 和
和![]() ,前后標桿相距
,前后標桿相距![]() 步,使后標桿桿腳
步,使后標桿桿腳![]() 與前標桿桿腳
與前標桿桿腳![]() 與山峰腳
與山峰腳![]() 在同一直線上,從前標桿桿腳
在同一直線上,從前標桿桿腳![]() 退行
退行![]() 步到
步到![]() ,人眼著地觀測到島峰,
,人眼著地觀測到島峰,![]() 、
、![]() 、
、![]() 三點共線,從后標桿桿腳
三點共線,從后標桿桿腳![]() 退行
退行![]() 步到
步到![]() ,人眼著地觀測到島峰,
,人眼著地觀測到島峰,![]() 、
、![]() 、
、![]() 三點也共線,問島峰的高度
三點也共線,問島峰的高度![]() 步. (古制:
步. (古制:![]() 步=
步=![]() 尺,
尺,![]() 里=
里=![]() 丈=
丈=![]() 尺=
尺=![]() 步)
步)
查看答案和解析>>
科目:高中數學 來源: 題型:
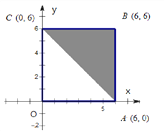
【題目】如圖:區域A是正方形OABC(含邊界),區域B是三角形ABC(含邊界)。
(Ⅰ)向區域A隨機拋擲一粒黃豆,求黃豆落在區域B的概率;
(Ⅱ)若x,y分別表示甲、乙兩人各擲一次骰子所得的點數,求點(x,y)落在區域B的概率;
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() 短軸頂點在圓
短軸頂點在圓![]() 上.
上.
(Ⅰ)求橢圓![]() 方程;
方程;
(Ⅱ)已知點![]() ,若斜率為1的直線
,若斜率為1的直線![]() 與橢圓
與橢圓![]() 相交于
相交于![]() 兩點,試探究以
兩點,試探究以![]() 為底邊的等腰三角形
為底邊的等腰三角形![]() 是否存在?若存在,求出直線
是否存在?若存在,求出直線![]() 的方程,若不存在,說明理由.
的方程,若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓的中心是坐標原點![]() ,焦點在
,焦點在![]() 軸上,離心率為
軸上,離心率為![]() ,又橢圓上任一點到兩焦點的距離和為
,又橢圓上任一點到兩焦點的距離和為![]() .過右焦點
.過右焦點![]() 與
與![]() 軸不垂直的直線
軸不垂直的直線![]() 交橢圓于
交橢圓于![]() ,
,![]() 兩點.
兩點.
(1)求橢圓的方程;
(2)在線段![]() 上是否存在點
上是否存在點![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的取值范圍;若不存在,請
的取值范圍;若不存在,請
說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com