
【題目】已知函數![]() 與
與![]() 互為相反數,且
互為相反數,且![]() ,函數
,函數![]() 的定義域為
的定義域為![]() .
.
(1)求![]() 的值;
的值;
(2)若![]() ,求
,求![]() 的值域;
的值域;
(3)若函數![]() 的最大值為
的最大值為![]() ,求實數
,求實數![]() 的值.
的值.
【答案】(1)a=log32.(2)[﹣2,0].(3)λ![]() .
.
【解析】
(1)先求得![]() ,再根據f(a+2)=18計算a;
,再根據f(a+2)=18計算a;
(2)令t=2x,結合二次函數閉區間上最值的求解即可.
(3)討論對稱軸與區間[1,2]的關系得出h(t)的單調性,根據最大值為![]() 計算λ.
計算λ.
(1)由題意函數![]() 與
與![]() 互為相反數,∴
互為相反數,∴![]() ,
,
又∵f(a+2)=3a+2=18,∴3a=2,即a=log32.
(2)當![]() 時,由(1)可知
時,由(1)可知![]() ,
,
令t=2x,
由x∈[0,1]可得t∈[1,2],g(t)=t﹣t2在[1,2]上單調遞減,
故當t=1時有最大值0,t=2時有最小值﹣2,
故值域[﹣2,0].
(3)∵函數![]() 的最大值為
的最大值為![]() ,由(2)可知:即為h(t)=﹣t2+λt,t∈[1,2]的最大值為
,由(2)可知:即為h(t)=﹣t2+λt,t∈[1,2]的最大值為![]() ,
,
①若![]() 2即λ≥4,則h(t)在[1,2]上單調遞增,
2即λ≥4,則h(t)在[1,2]上單調遞增,
∴h(2)=﹣4+2λ![]() ,解得λ
,解得λ![]() (舍).
(舍).
②若![]() 1即λ≤2時,則h(t)在[1,2]上單調遞減,
1即λ≤2時,則h(t)在[1,2]上單調遞減,
∴h(1)=﹣1+λ![]() ,解得λ
,解得λ![]() (舍).
(舍).
③若1![]() 2,即2<λ<4,則h(t)在[1,2]上先增后減,
2,即2<λ<4,則h(t)在[1,2]上先增后減,
∴h(![]() )
)![]() ,解得λ
,解得λ![]() (舍負).
(舍負).
綜上,λ![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】我國明代珠算家程大位的名著《直指算法統宗》中有如下問題:“今有白米一百八十石,令三人從上及和減率分之,只云甲多丙米三十六石,問:各該若干?”其意思為:“今有白米一百八十石,甲、乙、丙三人來分,他們分得的白米數構成等差數列,只知道甲比丙多分三十六石,那么三人各分得多少白米?”請問:乙應該分得( )白米
A. 96石B. 78石C. 60石D. 42石
查看答案和解析>>
科目:高中數學 來源: 題型:
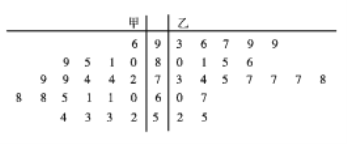
【題目】為推行“新課堂”教學法,某老師分別用傳統教學和“新課堂”兩種不同的教學方式在甲、乙兩個平行班進行教學實驗,為了解教學效果,期中考試后,分別從兩個班級中各隨機抽取20名學生的成績進行統計,作出如圖所示的莖葉圖,若成績大于70分為“成績優良”.
(1)由統計數據填寫下面2×2列聯表,并判斷能否在犯錯誤的概率不超過0.05的前提下認為“成績優良與教學方式有關”?
甲班 | 乙班 | 總計 | |
成績優良 | |||
成績不優良 | |||
總計 |
(2)從甲、乙兩班40個樣本中,成績在60分以下(不含60分)的學生中任意選取2人,求抽取的2人中恰有一人來自乙班的概率.
|
|
|
|
|
|
|
|
|
|
附:![]() ,(
,(![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=![]() ,下列結論中錯誤的是
,下列結論中錯誤的是
A. ![]()
![]() , f(
, f(![]() )=0
)=0
B. 函數y=f(x)的圖像是中心對稱圖形
C. 若![]() 是f(x)的極小值點,則f(x)在區間(-∞,
是f(x)的極小值點,則f(x)在區間(-∞,![]() )單調遞減
)單調遞減
D. 若![]() 是f(x)的極值點,則
是f(x)的極值點,則![]() (
(![]() )=0
)=0
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《九章算術》是我國古代的數學名著,書中把三角形的田稱為“圭田”,把直角梯形的田稱為“邪田”,稱底是“廣”,稱高是“正從”,“步”是丈量土地的單位.現有一邪田,廣分別為十步和二十步,正從為十步,其內有一塊廣為八步,正從為五步的圭田.若在邪田內隨機種植一株茶樹,求該株茶樹恰好種在圭田內的概率為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在直角坐標系![]() 中,以原點
中,以原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸建立極坐標系,圓
軸的正半軸為極軸建立極坐標系,圓![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求圓![]() 的直角坐標方程;
的直角坐標方程;
(2)設![]() ,直線
,直線![]() 的參數方程是
的參數方程是![]() (
(![]() 為參數),已知
為參數),已知![]() 與圓
與圓![]() 交于
交于![]() 兩點,且
兩點,且![]() ,求
,求![]() 的普通方程.
的普通方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在如圖所示的幾何體中,![]() 平面
平面![]() .
.
(1)證明:![]() 平面
平面![]() ;
;
(2)過點![]() 作一平行于平面
作一平行于平面![]() 的截面,畫出該截面,說明理由,并求夾在該截面與平面
的截面,畫出該截面,說明理由,并求夾在該截面與平面![]() 之間的幾何體的體積.
之間的幾何體的體積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com