
【題目】在△ABC中,已知B=45°,D是BC上一點,AD=5,AC=7,DC=3,求AB的長. 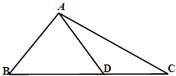
【答案】解:法一:在△ADC中,由余弦定理得: ![]() ∵∠ADC∈(0,π),∴∠ADC=120°,
∵∠ADC∈(0,π),∴∠ADC=120°,
∴∠ADB=180°﹣∠ADC=60°
在△ABD中,由正弦定理得: ![]()
法二:在△ADC中,由余弦定理得 ![]()
∵∠ACD∈(0,π),∴ ![]()
在△ABC中,由正弦定理得: 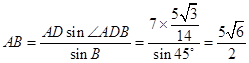
故答案為: ![]()
【解析】法一:先在△ADC中用余弦定理求出∠ADC的余弦值,進而求出∠ADC,再根據互補求出∠ADB,然后在△ABD中用正弦定理就可求出AB的長; 法二:先在△ADC中用余弦定理求出∠ACD的余弦值,在根據同角三角函數關系求出∠ACD的正弦,然后在△ABC中用正弦定理就可求出AB的長.
【考點精析】本題主要考查了正弦定理的定義和余弦定理的定義的相關知識點,需要掌握正弦定理:![]() ;余弦定理:
;余弦定理:![]() ;
;![]() ;
;![]() 才能正確解答此題.
才能正確解答此題.


科目:高中數學 來源: 題型:
【題目】已知橢圓C: ![]() =1(a>b>0)的離心率為
=1(a>b>0)的離心率為 ![]() ,且點
,且點 ![]() 在該橢圓上
在該橢圓上
(1)求橢圓C的方程;
(2)過橢圓C的左焦點F1的直線l與橢圓相交于A,B兩點,若△AOB的面積為 ![]() ,求圓心在原點O且與直線l相切的圓的方程.
,求圓心在原點O且與直線l相切的圓的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】有以下四種變換方式:
① 向左平移![]() 個單位長度,再將每個點的橫坐標縮短為原來的
個單位長度,再將每個點的橫坐標縮短為原來的![]() ;
;
② 向右平移![]() 個單位長度,再將每個點的橫坐標縮短為原來的
個單位長度,再將每個點的橫坐標縮短為原來的![]() ;
;
③ 每個點的橫坐標縮短為原來的![]() ,向右平移
,向右平移![]() 個單位長度;
個單位長度;
④ 每個點的橫坐標縮短為原來的![]() ,向左平移
,向左平移![]() 個單位長度;
個單位長度;
其中能將![]() 的圖像變換成函數
的圖像變換成函數![]() 的圖像的是( )
的圖像的是( )
A.①和③ B.①和④ C.②和④ D.②和③
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校從參加高三模擬考試的學生中隨機抽取60名學生,按其數學成績(均為整數)分成六組[90,100),[100,110),…,[140,150]后得到如下部分頻率分布直方圖,觀察圖中的信息,回答下列問題: 
(Ⅰ)補全頻率分布直方圖;
(Ⅱ)估計本次考試的數學平均成績(同一組中的數據用該組區間的中點值作代表);
(Ⅲ)用分層抽樣的方法在分數段為[110,130)的學生成績中抽取一個容量為6的樣本,再從這6個樣本中任取2人成績,求至多有1人成績在分數段[120,130)內的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知等差數列{an}的前n項和為Sn(n∈N*),a3=5,S10=100.
(1)求數列{an}的通項公式;
(2)設bn=2 ![]() +2n求數列{bn}的前n項和Tn .
+2n求數列{bn}的前n項和Tn .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() (
(![]() ,
, ![]() ),且對任意
),且對任意![]() ,都有
,都有![]() .
.
(Ⅰ)用含![]() 的表達式表示
的表達式表示![]() ;
;
(Ⅱ)若![]() 存在兩個極值點
存在兩個極值點![]() ,
, ![]() ,且
,且![]() ,求出
,求出![]() 的取值范圍,并證明
的取值范圍,并證明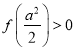 ;
;
(Ⅲ)在(Ⅱ)的條件下,判斷![]() 零點的個數,并說明理由.
零點的個數,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,內角A,B,C所對的邊分別為a,b,c,已知b+c=2acosB.
(Ⅰ)證明:A=2B
(Ⅱ)若△ABC的面積S= ![]() ,求角A的大小.
,求角A的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙兩位學生參加數學競賽培訓.現分別從他們在培訓期間參加的若干次預賽成績中隨機抽取5次,記錄如下:
甲 | 88 | 89 | 92 | 90 | 91 |
乙 | 84 | 88 | 96 | 89 | 93 |
(Ⅰ)用莖葉圖表示這兩組數據;
(Ⅱ)現要從中選派一人參加數學競賽,你認為選派哪位學生參加合適?請說明理由.(用樣本數據特征來說明.)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com