
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 為菱形,
為菱形,![]() 為正三角形,平面
為正三角形,平面![]() 平面
平面![]() 分別是
分別是![]() 的中點.
的中點.
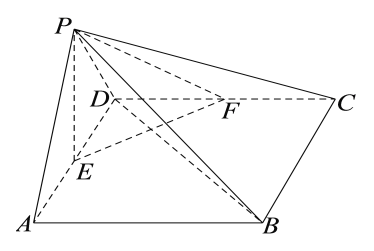
(1)證明:![]() 平面
平面![]()
(2)若![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】如圖,四棱錐P-ABCD的底面是矩形,PA⊥平面ABCD,E,F分別是AB,PD的中點,且PA=AD.
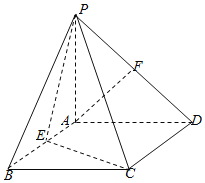
(Ⅰ)求證:AF∥平面PEC;
(Ⅱ)求證:平面PEC⊥平面PCD.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某單位計劃在一水庫建一座至多安裝3臺發電機的水電站,過去50年的水文資料顯示,水庫年入流量![]() (年入流量:一年內上游來水與庫區降水之和,單位:億立方米)都在40以上,不足80的年份有10年,不低于80且不超過120的年份有35年,超過120的年份有5年,將年入流量在以上三段的頻率作為相應段的概率,假設各年的年入流量相互獨立.
(年入流量:一年內上游來水與庫區降水之和,單位:億立方米)都在40以上,不足80的年份有10年,不低于80且不超過120的年份有35年,超過120的年份有5年,將年入流量在以上三段的頻率作為相應段的概率,假設各年的年入流量相互獨立.
(1)求未來3年中,設![]() 表示流量超過120的年數,求
表示流量超過120的年數,求![]() 的分布列及期望;
的分布列及期望;
(2)水電站希望安裝的發電機盡可能運行,但每年發電機最多可運行臺數受年入流量![]() 限制,并有如下關系:
限制,并有如下關系:
年入流量 |
|
|
|
發電機最多可運行臺數 | 1 | 2 | 3 |
若某臺發電機運行,則該臺年利潤為5000萬元,若某臺發電機未運行,則該臺年虧損800萬元,欲使水電站年總利潤的均值達到最大,應安裝發電機多少臺?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】德國著名數學家狄利克雷(Dirichlet,1805~1859)在數學領域成就顯著.19世紀,狄利克雷定義了一個“奇怪的函數” 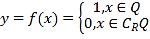 其中R為實數集,Q為有理數集.則關于函數
其中R為實數集,Q為有理數集.則關于函數![]() 有如下四個命題,正確的為( )
有如下四個命題,正確的為( )
A.函數![]() 是偶函數
是偶函數
B.![]() ,
,![]() ,
,![]() 恒成立
恒成立
C.任取一個不為零的有理數T,![]() 對任意的
對任意的![]() 恒成立
恒成立
D.不存在三個點![]() ,
,![]() ,
,![]() ,使得
,使得![]() 為等腰直角三角形
為等腰直角三角形
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com