
【題目】如圖,已知![]() 平面ABC,
平面ABC,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,點E和F分別為BC和
,點E和F分別為BC和![]() 的中點.
的中點.
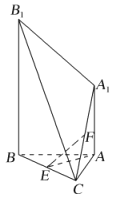
(1)求證:![]() 平面
平面![]() ;
;
(2)求證:直線![]() 平面
平面![]() ;
;
(3)求直線![]() 與平面
與平面![]() 所成角的大小.
所成角的大小.
【答案】(1)證明見解析;(2)證明見解析;(3)![]() .
.
【解析】
(1)連接![]() ,由題意易知
,由題意易知![]() ,再由線面平行的判定定理可得出結論;(2)結合題中條件利用線面垂直的判定定理直接判斷即可證明結論;(3)分別取
,再由線面平行的判定定理可得出結論;(2)結合題中條件利用線面垂直的判定定理直接判斷即可證明結論;(3)分別取![]() 的中點M,N,連接
的中點M,N,連接![]() ,
,![]() ,利用題中相關已知條件即可證明
,利用題中相關已知條件即可證明![]() ,利用(2)的結論可得
,利用(2)的結論可得![]() 面
面![]() ,則可得
,則可得![]() 就是直線
就是直線![]() 與平面
與平面![]() 所成的角,再結合題中數量關系可求得
所成的角,再結合題中數量關系可求得![]() =4,
=4,![]() ,則在
,則在![]() 中可得
中可得![]() ,則可得
,則可得![]() .
.
(1)證明:
如圖,連接![]() ,
,
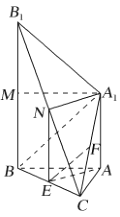
在![]() 中,因為E和F分別是BC和
中,因為E和F分別是BC和![]() 的中點,所以
的中點,所以![]() .
.
又因為EF平面![]() ,
,![]() 平面
平面![]() ,所以
,所以平面
![]() .
.
(2)證明:
因為![]() ,E為BC的中點,所以
,E為BC的中點,所以![]() .因為
.因為![]() 平面ABC,
平面ABC,![]() ,所以
,所以![]() 平面ABC,又
平面ABC,又![]() 平面ABC,從而
平面ABC,從而![]() .又因為
.又因為![]() ,
,
所以![]() 平面
平面![]() .
.
(3)解:取![]() 的中點M和
的中點M和![]() 的中點N,連接
的中點N,連接![]() ,
,![]() ,NE.因為N和E分別為
,NE.因為N和E分別為![]() 和BC的中點,所以
和BC的中點,所以![]() ,
,![]() ,故
,故![]() 且
且![]() ,所以
,所以![]() ,且
,且![]() .又因為
.又因為![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
從而![]() 為直線
為直線![]() 與平面
與平面![]() 所成的角.
所成的角.
在![]() 中,可得
中,可得![]() ,所以
,所以![]() .
.
因為![]() ,
,![]() ,
,
所以四邊形![]() 為平行四邊形,
為平行四邊形,
所以![]() ,
,![]() ,
,
又由![]() ,得
,得![]() .
.
在![]() 中,
中,
可得![]() .
.
在![]() 中,
中,
![]()
因此![]() .
.
所以直線![]() 與平面
與平面![]() 所成的角為30°.
所成的角為30°.


科目:高中數學 來源: 題型:
【題目】如圖,在四面體ABCD中,△ABC是等邊三角形,平面ABC⊥平面ABD,點M為棱AB的中點,AB=2,AD=![]() ,∠BAD=90°.
,∠BAD=90°.
(Ⅰ)求證:AD⊥BC;
(Ⅱ)求異面直線BC與MD所成角的余弦值;
(Ⅲ)求直線CD與平面ABD所成角的正弦值.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在如圖所示的幾何體中,![]() 平面
平面![]() .
.

(1)證明:![]() 平面
平面![]() ;
;
(2)過點![]() 作一平行于平面
作一平行于平面![]() 的截面,畫出該截面,說明理由,并求夾在該截面與平面
的截面,畫出該截面,說明理由,并求夾在該截面與平面![]() 之間的幾何體的體積.
之間的幾何體的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了調查某生產線上質量監督員甲是否在現場對產品質量好壞有無影響,現統計數據如下:質量監督員甲在現場時,1 000件產品中合格品有990件,次品有10件,甲不在現場時,500件產品中有合格品490件,次品有10件.
(1)補充下面列聯表,并初步判斷甲在不在現場與產品質量是否有關:
合格品數/件 | 次品數/件 | 總數/件 | |
甲在現場 | 990 | ||
甲不在現場 | 10 | ||
總數/件 |
(2)用獨立性檢驗的方法判斷能否在犯錯誤的概率不超過0.15的前提下認為“甲在不在現場與產品質量有關”?
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
K | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
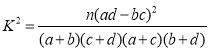
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知偶函數![]() 在區間
在區間![]() 上單調遞增,且滿
上單調遞增,且滿![]() ,給出下列判斷:
,給出下列判斷:
①![]() ;②
;②![]() 在
在![]() 上是減函數;③
上是減函數;③![]() 的圖象關于直線
的圖象關于直線![]() 對稱;
對稱;
④函數![]() 在
在![]() 處取得最大值;⑤函數
處取得最大值;⑤函數![]() 沒有最小值
沒有最小值
其中判斷正確的序號_______.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com