
【題目】在△ABC中,角A,B,C的對邊分別為a,b,c,cos C=.
(1)若·=,求c的最小值;
(2)設(shè)向量x=(2sin B,-),y=,且x∥y,求sin(B-A)的值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
試題分析:(1)借助題設(shè)條件運用向量的數(shù)量積公式及余弦定理求解;(2)借助題設(shè)運用向量平行建立方程,再利用三角變換公式探求.
試題解析:
(1) ∵ ·=![]() ,∴ abcosC=
,∴ abcosC=![]() ,∴ ab=15…………………..3分
,∴ ab=15…………………..3分
∴ c2=a2+b2-2abcosC≥2ab-2ab·![]() =21(當且僅當a=b時取等號).
=21(當且僅當a=b時取等號).
∵ c>0,∴ c≥![]() ,…………………………………………………………..5分
,…………………………………………………………..5分
∴ c的最小值為![]() …………………………………………………….7分
…………………………………………………….7分
(2) ∵ x∥y,∴ 2sin B![]() +
+![]() cos2B=0,
cos2B=0,
2sinBcosB+![]() cos2B=0,即sin 2B+
cos2B=0,即sin 2B+![]() cos2B=0,
cos2B=0,
∴ tan2B=-![]() ,∴ 2B=
,∴ 2B=![]() 或
或![]() ,∴ B=
,∴ B=![]() 或
或![]() ……………………10分
……………………10分
∵ cos C=![]() <
<![]() ,∴ C>
,∴ C>![]() ,
,
∴ B=![]() (舍去),∴ B=
(舍去),∴ B=![]() ……………………………………………..12分
……………………………………………..12分
∴ sin(B-A)=sin[B-(π-B-C)]
=sin![]() =sinCcos
=sinCcos![]() -cos Csin
-cos Csin![]()
=![]() ×
×![]() -
-![]() ×
×![]() =
=![]() …………………………………………..16分
…………………………………………..16分


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() ,其中
,其中![]() ,
,![]() .
.![]() 是自然對數(shù)的底數(shù).
是自然對數(shù)的底數(shù).
(1)求曲線![]() 在
在![]() 處的切線方程為
處的切線方程為![]() ,求實數(shù)
,求實數(shù)![]() ,
,![]() 的值;
的值;
(2)①若![]() 時,函數(shù)
時,函數(shù)![]() 既有極大值又有極小值,求實數(shù)
既有極大值又有極小值,求實數(shù)![]() 的取值范圍;
的取值范圍;
②若![]() ,
,![]() ,若
,若![]() 對一切正實數(shù)
對一切正實數(shù)![]() 恒成立,求實數(shù)
恒成立,求實數(shù)![]() 的取值范圍(用
的取值范圍(用![]() 表示).
表示).
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】先后2次拋擲一枚骰子,將得到的點數(shù)分別記為![]() .
.
(Ⅰ)求滿足![]() 的概率;
的概率;
(Ⅱ)設(shè)三條線段的長分別為![]() 和5,求這三條線段能圍成等腰三角形(含等邊三角形)的概率.
和5,求這三條線段能圍成等腰三角形(含等邊三角形)的概率.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】設(shè)函數(shù)![]() ,
, ![]() 表示
表示![]() 導函數(shù).
導函數(shù).
(1)當![]() 時,求函數(shù)
時,求函數(shù)![]() 在點
在點![]() 處的切線方程;
處的切線方程;
(2)討論函數(shù)![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(3)對于曲線![]() 上的不同兩點
上的不同兩點![]() ,求證:存在唯一的
,求證:存在唯一的![]() ,使直線
,使直線![]() 的斜率等于
的斜率等于![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某市統(tǒng)計局就某地居民的月收入調(diào)查了10000人,并根據(jù)所得數(shù)據(jù)畫出樣本的頻率分布直方圖,每個分組包括左端點,不包括右端點,如第一組表示收入在![]() .
.
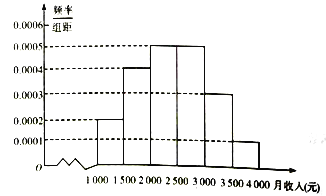
(1)求居民收入在![]() 的頻率;
的頻率;
(2)根據(jù)頻率分布直方圖算出樣本數(shù)據(jù)的中位數(shù)、平均數(shù)及其眾數(shù);
(3)為了分析居民的收入與年齡、職業(yè)等方面的關(guān)系,從這10000人中用分層抽樣方法抽出100人作進一步分析,則應月收入為![]() 的人中抽取多少人?
的人中抽取多少人?
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓![]() 的兩個焦點分別為
的兩個焦點分別為![]() ,
,![]() ,短軸的兩個端點分別為
,短軸的兩個端點分別為![]() ,
,![]() .
.
(1)若![]() 為等邊三角形,求橢圓
為等邊三角形,求橢圓![]() 的方程;
的方程;
(2)若橢圓![]() 的短軸長為2,過點
的短軸長為2,過點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 相交于
相交于![]() 、
、![]() 兩點,且
兩點,且![]() ,求直線
,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在平面直角坐標系![]() 中,橢圓
中,橢圓![]() 的離心率為
的離心率為![]() ,右頂點為
,右頂點為![]() ,直線
,直線![]() 過原點
過原點![]() ,且點
,且點![]() 在x軸的上方,直線
在x軸的上方,直線![]() 與
與![]() 分別交直線
分別交直線![]() :
: ![]() 于點
于點![]() 、
、![]() .
.
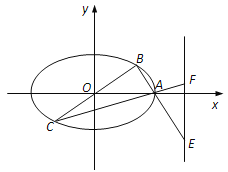
(1)若點![]() ,求橢圓的方程及△ABC的面積;
,求橢圓的方程及△ABC的面積;
(2)若![]() 為動點,設(shè)直線
為動點,設(shè)直線![]() 與
與![]() 的斜率分別為
的斜率分別為![]() 、
、![]() .
.
①試問![]() 是否為定值?若為定值,請求出;否則,請說明理由;
是否為定值?若為定值,請求出;否則,請說明理由;
②求△AEF的面積的最小值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在平面直角坐標系中,已知兩定點![]() 、
、![]() ,⊙C的方程為
,⊙C的方程為![]() .當⊙C的半徑取最小值時:
.當⊙C的半徑取最小值時:
(1)求出此時m的值,并寫出⊙C的標準方程;
(2)在x軸上是否存在異于點E的另外一個點F,使得對于⊙C上任意一點P,總有![]() 為定值?若存在,求出點F的坐標,若不存在,請說明你的理由;
為定值?若存在,求出點F的坐標,若不存在,請說明你的理由;
(3)在第(2)問的條件下,求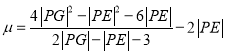 的取值范圍.
的取值范圍.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com