
【題目】求證: ![]() ﹣
﹣ ![]() <
< ![]() ﹣
﹣ ![]() (a≥3).
(a≥3).
科目:高中數學 來源: 題型:
【題目】設連續擲兩次骰子得到的點數分別為m、n,令平面向量 ![]() ,
, ![]() .
.
(1)求使得事件“ ![]() ”發生的概率;
”發生的概率;
(2)求使得事件“ ![]() ”發生的概率;
”發生的概率;
(3)使得事件“直線 ![]() 與圓(x﹣3)2+y2=1相交”發生的概率.
與圓(x﹣3)2+y2=1相交”發生的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數 ![]() 是定義在(﹣1,1)上的奇函數,且
是定義在(﹣1,1)上的奇函數,且 ![]() .
.
(1)確定函數的解析式;
(2)證明函數f(x)在(﹣1,1)上是增函數;
(3)解不等式f(t﹣1)+f(t)<0.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若實數![]() 滿足
滿足![]() ,則稱
,則稱![]() 為函數
為函數![]() 的不動點.
的不動點.
(1)求函數![]() 的不動點;
的不動點;
(2)設函數![]() ,其中
,其中![]() 為實數.
為實數.
① 若![]() 時,存在一個實數
時,存在一個實數![]() ,使得
,使得![]() 既是
既是![]() 的不動點,又是
的不動點,又是![]() 的不動點(
的不動點(![]() 是函數
是函數![]() 的導函數),求實數
的導函數),求實數![]() 的取值范圍;
的取值范圍;
② 令![]() ,若存在實數
,若存在實數![]() ,使
,使![]() ,
,![]() ,
,![]() ,
,![]() 成各項都為正數的等比數列,求證:函數
成各項都為正數的等比數列,求證:函數![]() 存在不動點.
存在不動點.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】PM2.5是指空氣中直徑小于或等于2.5微米的顆粒物(也稱可入肺顆粒物).為了探究車流量與PM2.5的濃度是否相關,現采集到某城市周一至周五某一時間段車流量與PM2.5的數據如表:
時間 | 周一 | 周二 | 周三 | 周四 | 周五 |
車流量x(萬輛) | 50 | 51 | 54 | 57 | 58 |
PM2.5的濃度y(微克/立方米) | 69 | 70 | 74 | 78 | 79 |
(1)根據上表數據,請在如圖坐標系中畫出散點圖; 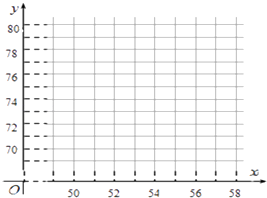
(2)根據上表數據,用最小二乘法求出y關于x的線性回歸方程 ![]() ;(保留2位小數)
;(保留2位小數)
(3)若周六同一時間段車流量是25萬輛,試根據(2)求出的線性回歸方程預測,此時PM2.5的濃度為多少(保留整數)?
參考公式: ![]() =
= 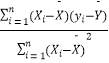 ,
, ![]() =
= ![]() ﹣
﹣ ![]()
![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=﹣x3+ax2+1,(a∈R).
(1)若f(x)圖象上橫坐標為1的點處存在垂直于y軸的切線,求a的值;
(2)若f(x)在區間(﹣1,2)內有兩個不同的極值點,求a取值范圍;
(3)當a=1時,是否存在實數m,使得函數g(x)=x4﹣5x3+(2﹣m)x2+1的圖象于函數f(x)的圖象恰有三個不同的交點,若存在,試求出實數m的值;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點F(0,1),直線l:y=﹣1,P為平面上的動點,過點P作直線l的垂線,垂足為Q,且 ![]() .
.
(1)求動點P的軌跡C的方程;
(2)已知圓M過定點D(0,2),圓心M在軌跡C上運動,且圓M與x軸交于A、B兩點,設|DA|=l1 , |DB|=l2 , 求 ![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com