
【題目】如圖,已知△![]() 的內角
的內角![]() 、
、![]() 、
、![]() 的對邊分別為
的對邊分別為![]() 、
、![]() 、
、![]() ,其中
,其中![]() ,且
,且![]() ,延長線段
,延長線段![]() 到點
到點![]() ,使得
,使得![]() ,
,![]() .
.
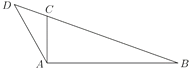
(1)求證:![]() 是直角;
是直角;
(2)求![]() 的值.
的值.
【答案】(1)證明見解析;(2)![]() .
.
【解析】
(1)根據正弦定理以及二倍角公式即可證明,
(2)如圖所示:過點C作CE⊥AC,根據平行線分線段成比例定理,設CE=x,則AB=5x,AD![]() x,再根據勾股定理可得x的值,再由正弦定理,sinD
x,再根據勾股定理可得x的值,再由正弦定理,sinD![]() ,再根據同角的三角函數的關系即可求出答案.
,再根據同角的三角函數的關系即可求出答案.
1)由正弦定理可得sinBcosB=sinCcosC,
即sin2B=sin2C,
∵b≠c,
∴2B+2C=180°,
∴B+C=90°,
∴∠BAC=180°﹣90°=90°,
(2)如圖所示:過點C作CE⊥AC,
∵BC=4,BC=4CD,
∴CD=1,BD=5,
∵∠BAC=90°,
∴CE∥AB,
∴![]() ,
,
設CE=x,則AB=5x,
∵∠CAD=30°,
∴AE=2x,AC![]() x,
x,
∴![]() ,
,
∴DE![]() x,
x,
∵AB2+AC2=BC2,
∴25x2+3x2=16,
解得x![]() ,
,
在△CED中,∠CED=120°,CE![]() ,CD=1,
,CD=1,
由正弦定理可得![]() ,
,
即sinD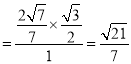 ,
,
cosD![]() ,
,
∴tanD![]() .
.


科目:高中數學 來源: 題型:
【題目】已知集合A={1,2,3,4}和集合B={1,2,3,…,n},其中n≥5,![]() .從集合A中任取三個不同的元素,其中最小的元素用S表示;從集合B中任取三個不同的元素,其中最大的元素用T表示.記X=T-S.
.從集合A中任取三個不同的元素,其中最小的元素用S表示;從集合B中任取三個不同的元素,其中最大的元素用T表示.記X=T-S.
(1)當n=5時,求隨機變量X的概率分布和數學期望![]() ;
;
(2)求![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ln![]() +ax﹣1(a≠0).
+ax﹣1(a≠0).
(I)求函數f(x)的單調區間;
(Ⅱ)已知g(x)+xf(x)=﹣x,若函數g(x)有兩個極值點x1,x2(x1<x2),求證:g(x1)<0.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若![]() 是遞增數列,數列
是遞增數列,數列![]() 滿足:對任意
滿足:對任意![]() ,存在
,存在![]() ,使得
,使得![]() ,則稱
,則稱![]() 是
是![]() 的“分隔數列”.
的“分隔數列”.
(1)設![]() ,證明:數列
,證明:數列![]() 是
是![]() 的分隔數列;
的分隔數列;
(2)設![]() 是
是![]() 的前n項和,
的前n項和,![]() ,判斷數列
,判斷數列![]() 是否是數列
是否是數列![]() 的分隔數列,并說明理由;
的分隔數列,并說明理由;
(3)設![]() 是
是![]() 的前n項和,若數列
的前n項和,若數列![]() 是
是![]() 的分隔數列,求實數
的分隔數列,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓:![]() 的左、右點分別為
的左、右點分別為![]() 點
點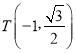 在橢圓上,且
在橢圓上,且![]()
(1)求橢圓![]() 的方程;
的方程;
(2)過點(1,0)作斜率為![]() 的直線
的直線![]() 交橢圓
交橢圓![]() 于M、N兩點,若
于M、N兩點,若![]() 求直線
求直線![]() 的方程;
的方程;
(3)點P、Q為橢圓上的兩個動點,![]() 為坐標原點,若直線
為坐標原點,若直線![]() 的斜率之積為
的斜率之積為![]() 求證:
求證:![]() 為定值.
為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知橢圓![]() :
:![]() ,左頂點為
,左頂點為![]() ,經過點
,經過點![]() ,過點
,過點![]() 作斜率為
作斜率為![]() 的直線
的直線![]() 交橢圓
交橢圓![]() 于點
于點![]() ,交
,交![]() 軸于點
軸于點![]() .
.
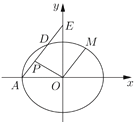
(1)求橢圓![]() 的方程;
的方程;
(2)已知![]() 為
為![]() 的中點,
的中點,![]() ,證明:對于任意的
,證明:對于任意的![]() 都有
都有![]() 恒成立;
恒成立;
(3)若過點![]() 作直線
作直線![]() 的平行線交橢圓
的平行線交橢圓![]() 于點
于點![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】![]() 統計學中將
統計學中將![]() 個數
個數![]() 的和記作
的和記作![]()
(1)設![]()
![]() ,求
,求![]() ;
;
(2)是否存在互不相等的非負整數![]() ,
,![]() ,使得
,使得![]() 成立,若存在,請寫出推理的過程;若不存在請證明;
成立,若存在,請寫出推理的過程;若不存在請證明;
(3)設![]()
![]() 是不同的正實數,
是不同的正實數,![]() ,對任意的
,對任意的![]() ,都有
,都有![]() ,判斷
,判斷![]() 是否為一個等比數列,請說明理由.
是否為一個等比數列,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于定義在![]() 上的函數
上的函數![]() ,如果存在兩條平行直線
,如果存在兩條平行直線![]() 與
與![]()
![]() ,使得對于任意
,使得對于任意![]() ,都有
,都有![]() 恒成立,那么稱函數
恒成立,那么稱函數![]() 是帶狀函數,若
是帶狀函數,若![]() ,
,![]() 之間的最小距離
之間的最小距離![]() 存在,則稱
存在,則稱![]() 為帶寬.
為帶寬.
(1)判斷函數![]() 是不是帶狀函數?如果是,指出帶寬(不用證明);如果不是,說明理由;
是不是帶狀函數?如果是,指出帶寬(不用證明);如果不是,說明理由;
(2)求證:函數![]() (
(![]() )是帶狀函數;
)是帶狀函數;
(3)求證:函數![]() (
(![]() )為帶狀函數的充要條件是
)為帶狀函數的充要條件是![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com